题目内容
把边长为6的等边三角形铁皮剪去三个相同的四边形(如图阴影部分)后,用剩余部分做成一个无盖的正三棱柱形容器(不计接缝),设容器的高为x,容积为V(x).(1)写出函数V(x)的解析式,并求出函数的定义域;
(2)求当x为多少时,容器的容积最大?并求出最大容积.
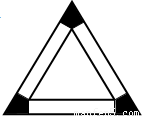
【答案】分析:(1)由已知中容器的高为x,正三棱柱形容器的底边长为 ,我们计算出棱柱的底面面积代入棱柱体积公式,即可求出函数V(x)的解析式,并根据高和底面边长均为正和,可以得到函数的解析式.
,我们计算出棱柱的底面面积代入棱柱体积公式,即可求出函数V(x)的解析式,并根据高和底面边长均为正和,可以得到函数的解析式.
(2)由(1)的中的解析式,我们求出函数导函数的解析式,利用导数法,求出函数的极值点,分析函数的单调性,即可得到当x为多少时,容器的容积最大,代入即可得到最大容积.
解答:解:(1)因为容器的高为x,则做成的正三棱柱形容器的底边长为 (1分).
(1分).
则 (4分)
(4分)
函数的定义域为 (5分)
(5分)
(2)实际问题归结为求函数V(x)在区间 上的最大值点.先求V(x)的极值点.
上的最大值点.先求V(x)的极值点.
在开区间 内,
内, (7分)
(7分)
令V′(x)=0,即令 ,解得
,解得 .
.
因为 在区间
在区间 内,x1可能是极值点.当0<x<x1时,V′(x)>0;
内,x1可能是极值点.当0<x<x1时,V′(x)>0;
当 时,V′(x)<0.(9分)
时,V′(x)<0.(9分)
因此x1是极大值点,且在区间 内,x1是唯一的极值点,
内,x1是唯一的极值点,
所以 是V(x)的最大值点,并且最大值
是V(x)的最大值点,并且最大值 
即当正三棱柱形容器高为 时,容器的容积最大为4.
时,容器的容积最大为4.
点评:本题考查的知识点是函数模型的选择与应用,其中解答本题的关键是根据已知求出棱柱的底面面积和高,进而求出函数的解析式,建立数学模型.
 ,我们计算出棱柱的底面面积代入棱柱体积公式,即可求出函数V(x)的解析式,并根据高和底面边长均为正和,可以得到函数的解析式.
,我们计算出棱柱的底面面积代入棱柱体积公式,即可求出函数V(x)的解析式,并根据高和底面边长均为正和,可以得到函数的解析式.(2)由(1)的中的解析式,我们求出函数导函数的解析式,利用导数法,求出函数的极值点,分析函数的单调性,即可得到当x为多少时,容器的容积最大,代入即可得到最大容积.
解答:解:(1)因为容器的高为x,则做成的正三棱柱形容器的底边长为
 (1分).
(1分).则
 (4分)
(4分)函数的定义域为
 (5分)
(5分)(2)实际问题归结为求函数V(x)在区间
 上的最大值点.先求V(x)的极值点.
上的最大值点.先求V(x)的极值点.在开区间
 内,
内, (7分)
(7分)令V′(x)=0,即令
 ,解得
,解得 .
.因为
 在区间
在区间 内,x1可能是极值点.当0<x<x1时,V′(x)>0;
内,x1可能是极值点.当0<x<x1时,V′(x)>0;当
 时,V′(x)<0.(9分)
时,V′(x)<0.(9分)因此x1是极大值点,且在区间
 内,x1是唯一的极值点,
内,x1是唯一的极值点,所以
 是V(x)的最大值点,并且最大值
是V(x)的最大值点,并且最大值 
即当正三棱柱形容器高为
 时,容器的容积最大为4.
时,容器的容积最大为4.点评:本题考查的知识点是函数模型的选择与应用,其中解答本题的关键是根据已知求出棱柱的底面面积和高,进而求出函数的解析式,建立数学模型.

练习册系列答案
相关题目
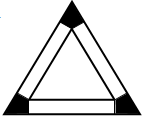 把边长为6的等边三角形铁皮剪去三个相同的四边形(如图阴影部分)后,用剩余部分做成一个无盖的正三棱柱形容器(不计接缝),设容器的高为x,容积为V(x).
把边长为6的等边三角形铁皮剪去三个相同的四边形(如图阴影部分)后,用剩余部分做成一个无盖的正三棱柱形容器(不计接缝),设容器的高为x,容积为V(x). 把边长为6的等边三角形铁皮剪去三个相同的四边形(如图阴影部分)后,用剩余部分做成一个无盖的正三棱柱形容器(不计接缝),设容器的高为x,容积为V(x).
把边长为6的等边三角形铁皮剪去三个相同的四边形(如图阴影部分)后,用剩余部分做成一个无盖的正三棱柱形容器(不计接缝),设容器的高为x,容积为V(x).
