题目内容
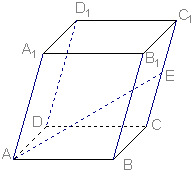
如图，在平行六面体ABCD-A1B1C1D1中，AB=5，AD=3，AA1=4，∠DAB=90°，∠BAA1=∠DAA1=60°，E是CC1的中点，设
=
，
=
，
=
．
（1）用
，
，
表示
；
（2）求AE的长？
| AB |
| a |
| AD |
| b |
| AA1 |
| c |
（1）用
| a |
| b |
| c |
| AE |
（2）求AE的长？
（1）根据向量的三角形法则得到
=
+
+
=
+
+
（2）∵|
|2=(
+
+
)2
=
2+
2+
2+2
•
+
•
+
•
=25+9+4+0+（20+12）•cos60°
=54
∴|
|=3
，
即AE的长为3
．
| AE |
| AB |
| BC |
| CE |
| a |
| b |
| 1 |
| 2 |
| c |
（2）∵|
| AE |
| a |
| b |
| 1 |
| 2 |
| c |
=
| a |
| b |
| 1 |
| 4 |
| c |
| a |
| b |
| a |
| c |
| b |
| c |
=25+9+4+0+（20+12）•cos60°
=54
∴|
| AE |
| 6 |
即AE的长为3
| 6 |
练习册系列答案
相关题目
．
证明：
；
,求
．
点C在
内部且
，设
，则
等于（ ）.
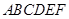中，动圆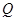
的半径为1，圆心在线段
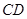（含端点）上运动，
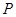是圆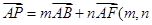
为实数），则
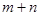的最大值为____________．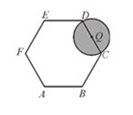
的面积为2，在
、
，满足
,
,则
的面积为（ ）
，则
的最小值是_______________．
中，点
是
上的点，
,则（ ）.
，
，则
在
方向上的投影取值范围是_____________．