题目内容
已知函数f(x)在定义域R内是增函数,且f(x)<0,则g(x)=x2 f(x)的单调情况一定是( )
| A.在(-∞,0)上递增 | B.在(-∞,0)上递减 |
| C.在R上递减 | D.在R上递增 |
A
解析试题分析:因为,函数f(x)在定义域R内是增函数,所以, ,又f(x)<0,所以,
,又f(x)<0,所以, >0,在(-∞,0)成立,即g(x)=x2 f(x)的单调情况一定是在(-∞,0)上递增,故选A.
>0,在(-∞,0)成立,即g(x)=x2 f(x)的单调情况一定是在(-∞,0)上递增,故选A.
考点:本题主要考查导数的运算法则,导数的应用。
点评:简单题,函数在某区间为增函数,则函数的导数非负;函数在某区间为减函数,则函数的导数非正。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
设函数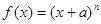 ,其中
,其中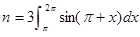 ,
,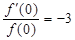 ,则
,则 的展开式中
的展开式中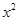 的系数为( )
的系数为( )
A.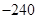 | B.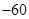 | C.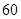 | D.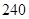 |
设曲线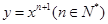 在点(1,1)处的切线与x轴的交点的横坐标为
在点(1,1)处的切线与x轴的交点的横坐标为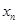 ,则
,则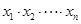 的值为
的值为
A.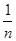 | B.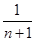 | C.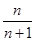 | D.1 |
一个物体的运动方程为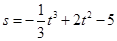 ,其中
,其中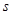 的单位是米,
的单位是米,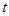 的单位是秒,那么物体在3秒末的瞬时速度是( )
的单位是秒,那么物体在3秒末的瞬时速度是( )
| A.3米/秒 | B.6米/秒 | C.5米/秒 | D.4米/秒 |
根据定积分的几何意义,计算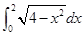 的结果是( )
的结果是( )
A.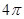 | B.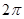 | C.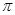 | D.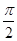 |
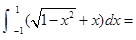 ( )
( )
A.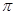 | B.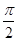 | C.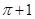 | D.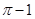 |
设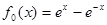 ,且对任意的
,且对任意的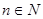 ,都有
,都有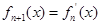 ,则
,则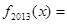
A.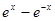 | B.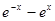 | C.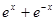 | D.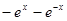 |
设函数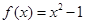 ,则
,则 在
在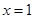 处的导数
处的导数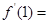 ( )
( )
A.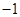 | B.0 | C.1 | D.2 |
 ,则
,则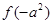 与
与 的大小关系为( )
的大小关系为( ) B.
B.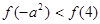
 D
D