题目内容
已知数列 满足:
满足: ,
,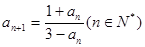
(Ⅰ)计算 的值;
的值;
(Ⅱ)由(Ⅰ)的结果猜想 的通项公式,并用数学归纳法证明你的结论.
的通项公式,并用数学归纳法证明你的结论.
【解析】本试题主要考查了数列的通项公式的求解和猜想和数学归纳法的证明。
【答案】
解:(Ⅰ) 由 ,
,
当n=1时,
当n=2时,
 当n=3时,
当n=3时, 4分
4分
(Ⅱ)由(Ⅰ)猜想 6分证明:(1) 当n=1时,
6分证明:(1) 当n=1时, 成立 7分
成立 7分
(2)假设n=k时, 成立那么,当n=k+1时有
成立那么,当n=k+1时有 即n=k+1时成立.
10分
即n=k+1时成立.
10分
综合(1) 和(2),由数学归纳法可知 成立.
成立.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 满足
满足 ,则此数列的通项
,则此数列的通项 等于
等于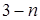 B.
B. C.
C.  D.
D. 
 满足:
满足: .
. ;
; ,求数列
,求数列 的通项公式;
的通项公式; ,不等式
,不等式 恒成立时,求实数
恒成立时,求实数 的取值范围.
的取值范围.