题目内容
已知函数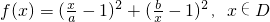 ,其中0<a<b.
,其中0<a<b.
(1)当D=(0,+∞)时,设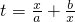 ,f(x)=g(t),求y=g(t)的解析式及定义域;
,f(x)=g(t),求y=g(t)的解析式及定义域;
(2)当D=(0,+∞),a=1,b=2时,求f(x)的最小值;
(3)设k>0,当a=k2,b=(k+1)2时,1≤f(x)≤9对任意x∈[a,b]恒成立,求k的取值范围.
解:(1)∵t= +
+ ,0<a<b,x>0,
,0<a<b,x>0,
∴t≥2 =
= ,
,
又f(x)= +
+ =
= +1-
+1-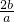 ,f(x)=g(t),
,f(x)=g(t),
∴g(t)=(t-1)2+1-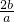 ,t∈[
,t∈[ ,+∞);
,+∞);
(2)∵x>0,a=1,b=2,
∴f(x)= -3,又x+
-3,又x+ -1≥2
-1≥2 -1(当且仅当x=
-1(当且仅当x= 时取“=”)
时取“=”)
∴f(x)≥ -3=6-4
-3=6-4 ,
,
∴f(x)min=6-4 .
.
(3)由题意可得,x∈[a,b]=[k2,(k+1)2],1≤f(x)≤9恒成立,
∴只需求得x∈[k2,(k+1)2]时f(x)的最小值即可.
∵此时,f(x)= +1-
+1- ,
,
∵k>0,x>0,令g(x)= +
+ =
=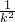 (x+
(x+ )≥
)≥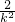 •k(k+1)=2
•k(k+1)=2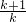 (当且仅当x=k(k+1)时取“=”).
(当且仅当x=k(k+1)时取“=”).
∴g(x)min= ,由题意可知,当g(x)取到最小值时,f(x)取到最小值.
,由题意可知,当g(x)取到最小值时,f(x)取到最小值.
∴f(x)min= +1-
+1- =
=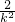 ,
,
∴1≤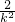 ≤9,而k>0,
≤9,而k>0,
∴ ≤k≤
≤k≤ .
.
分析:(1)由题意可得f(x)= +1-
+1-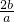 ,而t=
,而t= +
+ ,于是可得y=g(t)的解析式及定义域;
,于是可得y=g(t)的解析式及定义域;
(2)a=1,b=2时,f(x)= -3,利用x+
-3,利用x+ -1≥2
-1≥2 -1即可求得f(x)的最小值;
-1即可求得f(x)的最小值;
(3)由题意可求得x∈[a,b]=[k2,(k+1)2]时,f(x)min=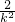 ,由1≤
,由1≤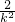 ≤9,k>0,即可求得k的取值范围.
≤9,k>0,即可求得k的取值范围.
点评:本题考查基本不等式,考查函数恒成立问题,考查二次函数的性质,考查综合分析与运算能力,难度大,属于难题.
 +
+ ,0<a<b,x>0,
,0<a<b,x>0,∴t≥2
 =
= ,
,又f(x)=
 +
+ =
= +1-
+1-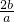 ,f(x)=g(t),
,f(x)=g(t),∴g(t)=(t-1)2+1-
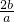 ,t∈[
,t∈[ ,+∞);
,+∞);(2)∵x>0,a=1,b=2,
∴f(x)=
 -3,又x+
-3,又x+ -1≥2
-1≥2 -1(当且仅当x=
-1(当且仅当x= 时取“=”)
时取“=”)∴f(x)≥
 -3=6-4
-3=6-4 ,
,∴f(x)min=6-4
 .
.(3)由题意可得,x∈[a,b]=[k2,(k+1)2],1≤f(x)≤9恒成立,
∴只需求得x∈[k2,(k+1)2]时f(x)的最小值即可.
∵此时,f(x)=
 +1-
+1- ,
,∵k>0,x>0,令g(x)=
 +
+ =
=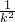 (x+
(x+ )≥
)≥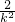 •k(k+1)=2
•k(k+1)=2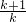 (当且仅当x=k(k+1)时取“=”).
(当且仅当x=k(k+1)时取“=”).∴g(x)min=
 ,由题意可知,当g(x)取到最小值时,f(x)取到最小值.
,由题意可知,当g(x)取到最小值时,f(x)取到最小值.∴f(x)min=
 +1-
+1- =
=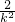 ,
,∴1≤
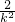 ≤9,而k>0,
≤9,而k>0,∴
 ≤k≤
≤k≤ .
.分析:(1)由题意可得f(x)=
 +1-
+1-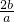 ,而t=
,而t= +
+ ,于是可得y=g(t)的解析式及定义域;
,于是可得y=g(t)的解析式及定义域;(2)a=1,b=2时,f(x)=
 -3,利用x+
-3,利用x+ -1≥2
-1≥2 -1即可求得f(x)的最小值;
-1即可求得f(x)的最小值;(3)由题意可求得x∈[a,b]=[k2,(k+1)2]时,f(x)min=
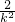 ,由1≤
,由1≤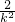 ≤9,k>0,即可求得k的取值范围.
≤9,k>0,即可求得k的取值范围.点评:本题考查基本不等式,考查函数恒成立问题,考查二次函数的性质,考查综合分析与运算能力,难度大,属于难题.

练习册系列答案
相关题目
 ,其中0<a<b.
,其中0<a<b. ,f(x)=g(t),求y=g(t)的解析式及定义域;
,f(x)=g(t),求y=g(t)的解析式及定义域;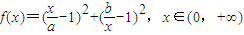 ,其中0<a<b.
,其中0<a<b.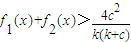 .
.