题目内容
已知函数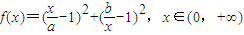 ,其中0<a<b.
,其中0<a<b.(1)当a=1,b=2时,求f(x)的最小值;
(2)若f(a)≥2m-1对任意0<a<b恒成立,求实数m的取值范围;
(3)设k、c>0,当a=k2,b=(k+c)2时,记f(x)=f1(x);当a=(k+c)2,b=(k+2c)2时,记f(x)=f2(x).
求证:
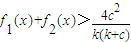 .
.
【答案】分析:(1)当a=1,b=2时,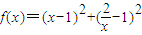 =(x2+
=(x2+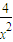 )-2(
)-2(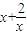 )+2,利用换元法,转化为二次函数,利用单调性,可求f(x)的最小值;
)+2,利用换元法,转化为二次函数,利用单调性,可求f(x)的最小值;
(2)f(x)≥2m-1对任意0<a<b恒成立,等价于f(x)min≥2m-1,函数可化为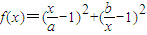 =
=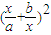 -2(
-2(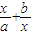 )-
)-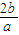 +2,利用换元法,转化为二次函数,利用单调性,即可求实数m的取值范围;
+2,利用换元法,转化为二次函数,利用单调性,即可求实数m的取值范围;
(3)利用基本不等式可得 (a2+b2)≥
(a2+b2)≥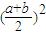 ,从而可得
,从而可得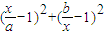 >
>
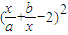 >2
>2 ,利用条件再利用基本不等式,即可证得结论.
,利用条件再利用基本不等式,即可证得结论.
解答:解:(1)当a=1,b=2时,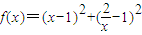 =(x2+
=(x2+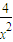 )-2(
)-2(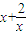 )+2
)+2
令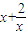 =t(t≥2
=t(t≥2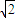 ),y=t2-2t-2=(t-1)2-3
),y=t2-2t-2=(t-1)2-3
∴函数在[2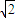 ,+∞)上单调增,∴y≥6-4
,+∞)上单调增,∴y≥6-4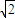
∴f(x)的最小值为6-4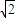 ;
;
(2)f(x)≥2m-1对任意0<a<b恒成立,等价于f(x)min≥2m-1
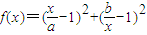 =
=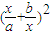 -2(
-2(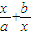 )-
)-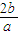 +2
+2
令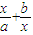 =t(t≥
=t(t≥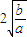 ),则y=t2-2t-
),则y=t2-2t-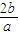 +2
+2
∴函数在[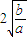 ,+∞)上单调增,∴y≥
,+∞)上单调增,∴y≥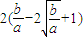 >0
>0
∴0≥2m-1
∴m≤0;
(3)因为 (a2+b2)≥
(a2+b2)≥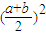 ,所以
,所以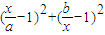 >
>
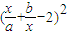 >2
>2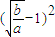
当a=k2,b=(k+c)2时,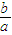 =
=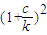 ;当a=(k+c)2,b=(k+2c)2时,
;当a=(k+c)2,b=(k+2c)2时,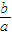 =
=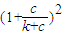
所以f1(x)+f2(x)>2(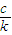 )2+2(
)2+2(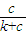 )2)>
)2)>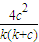 (因为0<a<b,所以等号取不到)
(因为0<a<b,所以等号取不到)
点评:本题考查基本不等式的运用,考查函数的单调性,多次应用了基本不等式,注意等号成立的条件.
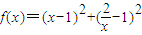 =(x2+
=(x2+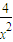 )-2(
)-2(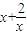 )+2,利用换元法,转化为二次函数,利用单调性,可求f(x)的最小值;
)+2,利用换元法,转化为二次函数,利用单调性,可求f(x)的最小值;(2)f(x)≥2m-1对任意0<a<b恒成立,等价于f(x)min≥2m-1,函数可化为
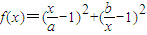 =
=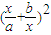 -2(
-2(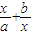 )-
)-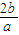 +2,利用换元法,转化为二次函数,利用单调性,即可求实数m的取值范围;
+2,利用换元法,转化为二次函数,利用单调性,即可求实数m的取值范围;(3)利用基本不等式可得
 (a2+b2)≥
(a2+b2)≥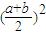 ,从而可得
,从而可得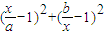 >
>
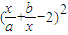 >2
>2 ,利用条件再利用基本不等式,即可证得结论.
,利用条件再利用基本不等式,即可证得结论.解答:解:(1)当a=1,b=2时,
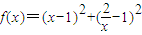 =(x2+
=(x2+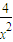 )-2(
)-2(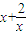 )+2
)+2令
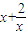 =t(t≥2
=t(t≥2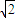 ),y=t2-2t-2=(t-1)2-3
),y=t2-2t-2=(t-1)2-3∴函数在[2
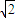 ,+∞)上单调增,∴y≥6-4
,+∞)上单调增,∴y≥6-4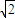
∴f(x)的最小值为6-4
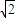 ;
;(2)f(x)≥2m-1对任意0<a<b恒成立,等价于f(x)min≥2m-1
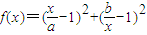 =
=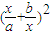 -2(
-2(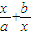 )-
)-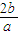 +2
+2令
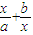 =t(t≥
=t(t≥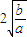 ),则y=t2-2t-
),则y=t2-2t-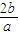 +2
+2∴函数在[
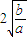 ,+∞)上单调增,∴y≥
,+∞)上单调增,∴y≥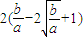 >0
>0∴0≥2m-1
∴m≤0;
(3)因为
 (a2+b2)≥
(a2+b2)≥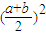 ,所以
,所以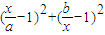 >
>
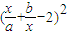 >2
>2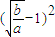
当a=k2,b=(k+c)2时,
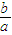 =
=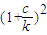 ;当a=(k+c)2,b=(k+2c)2时,
;当a=(k+c)2,b=(k+2c)2时,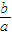 =
=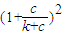
所以f1(x)+f2(x)>2(
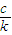 )2+2(
)2+2(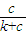 )2)>
)2)>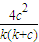 (因为0<a<b,所以等号取不到)
(因为0<a<b,所以等号取不到)点评:本题考查基本不等式的运用,考查函数的单调性,多次应用了基本不等式,注意等号成立的条件.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案
相关题目
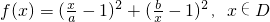 ,其中0<a<b.
,其中0<a<b.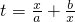 ,f(x)=g(t),求y=g(t)的解析式及定义域;
,f(x)=g(t),求y=g(t)的解析式及定义域; ,其中0<a<b.
,其中0<a<b. ,f(x)=g(t),求y=g(t)的解析式及定义域;
,f(x)=g(t),求y=g(t)的解析式及定义域;