题目内容
(12分)若![]() ,
,![]() ,其中
,其中![]() ,函数
,函数![]() ,且
,且![]() 的图象关于直线
的图象关于直线![]() 对称.
对称.
(1)求![]() 的解析式及
的解析式及![]() 的单调区间;
的单调区间;
(2)将![]() 的图象向左平移
的图象向左平移![]() 个单位,再将得到的图象的横坐标变为原来的2倍(纵坐标不变)后得到的
个单位,再将得到的图象的横坐标变为原来的2倍(纵坐标不变)后得到的![]() 的图象;若函数
的图象;若函数![]() ,
,![]() 的图象与
的图象与![]() 的图象有三个交点且交点的横坐标成等比数列,求
的图象有三个交点且交点的横坐标成等比数列,求![]() 的值.
的值.
解析:(1)∵![]() ,
,![]()
∴![]()
![]()
![]()
![]() ∵
∵![]() 的图象关于直线
的图象关于直线![]() 对称,
对称,
∴![]() ,解得
,解得![]() ∵
∵![]() ,∴
,∴![]() ,∴
,∴![]() , ∴
, ∴![]() ∴
∴![]()
(2)将![]() 的图象向左平移
的图象向左平移![]() 个单位后,得到
个单位后,得到![]()
![]() ,再将得到的图象的横坐标变为原来的2倍(纵坐标不变)后,得到
,再将得到的图象的横坐标变为原来的2倍(纵坐标不变)后,得到![]()
函数![]() ,
,![]() 的图象与
的图象与![]() 的图象有三个交点坐标分别为
的图象有三个交点坐标分别为![]() 且
且![]() ,
,
则由已知结合如图图象的对称性有 ,解得
,解得![]() ∴
∴![]()

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
 为
为 上的奇函数,且满足
上的奇函数,且满足 ,对于下列命题:
,对于下列命题: ;
;  对称;
对称;  .
.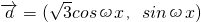 ,
,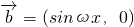 ,其中
,其中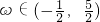 ,函数
,函数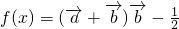 ,且f(x)的图象关于直线
,且f(x)的图象关于直线 对称.
对称. 个单位,再将得到的图象的横坐标变为原来的2倍(纵坐标不变)后得到的y=g(x)的图象;若函数y=g(x),
个单位,再将得到的图象的横坐标变为原来的2倍(纵坐标不变)后得到的y=g(x)的图象;若函数y=g(x),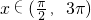 的图象与y=a的图象有三个交点且交点的横坐标成等比数列,求a的值.
的图象与y=a的图象有三个交点且交点的横坐标成等比数列,求a的值.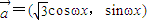 ,
,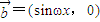 ,其中
,其中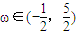 ,函数
,函数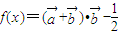 ,且f(x)的图象关于直线
,且f(x)的图象关于直线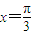 对称.
对称.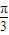 个单位,再将得到的图象的横坐标变为原来的2倍(纵坐标不变)后得到的y=g(x)的图象;若函数y=g(x),
个单位,再将得到的图象的横坐标变为原来的2倍(纵坐标不变)后得到的y=g(x)的图象;若函数y=g(x),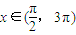 的图象与y=a的图象有三个交点且交点的横坐标成等比数列,求a的值.
的图象与y=a的图象有三个交点且交点的横坐标成等比数列,求a的值. ,
, ,其中
,其中 ,函数
,函数 ,且f(x)的图象关于直线
,且f(x)的图象关于直线 对称.
对称. 个单位,再将得到的图象的横坐标变为原来的2倍(纵坐标不变)后得到的y=g(x)的图象;若函数y=g(x),
个单位,再将得到的图象的横坐标变为原来的2倍(纵坐标不变)后得到的y=g(x)的图象;若函数y=g(x), 的图象与y=a的图象有三个交点且交点的横坐标成等比数列,求a的值.
的图象与y=a的图象有三个交点且交点的横坐标成等比数列,求a的值.