题目内容
若 ,
, ,其中
,其中 ,函数
,函数 ,且f(x)的图象关于直线
,且f(x)的图象关于直线 对称.
对称.(1)求f(x)的解析式及f(x)的单调区间;
(2)将y=f(x)的图象向左平移
 个单位,再将得到的图象的横坐标变为原来的2倍(纵坐标不变)后得到的y=g(x)的图象;若函数y=g(x),
个单位,再将得到的图象的横坐标变为原来的2倍(纵坐标不变)后得到的y=g(x)的图象;若函数y=g(x), 的图象与y=a的图象有三个交点且交点的横坐标成等比数列,求a的值.
的图象与y=a的图象有三个交点且交点的横坐标成等比数列,求a的值.
【答案】分析:(1)根据函数 ,把向量
,把向量 ,
, ,代入化简,利用f(x)的图象关于直线
,代入化简,利用f(x)的图象关于直线 对称求出ω,得到函数f(x)的表达式.
对称求出ω,得到函数f(x)的表达式.
(2)按照将y=f(x)的图象向左平移 个单位,再将得到的图象的横坐标变为原来的2倍(纵坐标不变)后,求出函数
个单位,再将得到的图象的横坐标变为原来的2倍(纵坐标不变)后,求出函数
y=g(x)的图象;求出函数y=g(x), 的范围,图象与y=a的图象有三个交点且交点的横坐标成等比数列,列出方程,求a的值.
的范围,图象与y=a的图象有三个交点且交点的横坐标成等比数列,列出方程,求a的值.
解答:解:(1)∵ ,
,
∴
 =
= =
=
∵f(x)的图象关于直线 对称,
对称,
∴ ,解得
,解得
∵ ,∴
,∴ ,∴-1<k<1(k∈Z),∴k=0,ω=1
,∴-1<k<1(k∈Z),∴k=0,ω=1
∴
(2)将 的图象向左平移
的图象向左平移 个单位后,
个单位后,
得到 =
= ,
,
再将得到的图象的横坐标变为原来的2倍(纵坐标不变)后,得到y=g(x)=cosx
函数y=g(x)=cosx, 的图象与y=a的图象有三个交点坐标分别为(x1,a),(x2,a),(x3,a)且
的图象与y=a的图象有三个交点坐标分别为(x1,a),(x2,a),(x3,a)且 ,
,
则由已知结合如图图象的对称性有 ,解得
,解得
∴
点评:本题考查函数y=Asin(ωx+φ)的图象变换,平面向量数量积的运算,正弦函数的单调性,考查计算能力,考查数形结合思想.
 ,把向量
,把向量 ,
, ,代入化简,利用f(x)的图象关于直线
,代入化简,利用f(x)的图象关于直线 对称求出ω,得到函数f(x)的表达式.
对称求出ω,得到函数f(x)的表达式.(2)按照将y=f(x)的图象向左平移
 个单位,再将得到的图象的横坐标变为原来的2倍(纵坐标不变)后,求出函数
个单位,再将得到的图象的横坐标变为原来的2倍(纵坐标不变)后,求出函数y=g(x)的图象;求出函数y=g(x),
 的范围,图象与y=a的图象有三个交点且交点的横坐标成等比数列,列出方程,求a的值.
的范围,图象与y=a的图象有三个交点且交点的横坐标成等比数列,列出方程,求a的值.解答:解:(1)∵
 ,
,
∴

 =
= =
=
∵f(x)的图象关于直线
 对称,
对称,∴
 ,解得
,解得
∵
 ,∴
,∴ ,∴-1<k<1(k∈Z),∴k=0,ω=1
,∴-1<k<1(k∈Z),∴k=0,ω=1∴

(2)将
 的图象向左平移
的图象向左平移 个单位后,
个单位后,得到
 =
= ,
,再将得到的图象的横坐标变为原来的2倍(纵坐标不变)后,得到y=g(x)=cosx
函数y=g(x)=cosx,
 的图象与y=a的图象有三个交点坐标分别为(x1,a),(x2,a),(x3,a)且
的图象与y=a的图象有三个交点坐标分别为(x1,a),(x2,a),(x3,a)且 ,
,则由已知结合如图图象的对称性有
 ,解得
,解得
∴

点评:本题考查函数y=Asin(ωx+φ)的图象变换,平面向量数量积的运算,正弦函数的单调性,考查计算能力,考查数形结合思想.

练习册系列答案
相关题目
 为
为 上的奇函数,且满足
上的奇函数,且满足 ,对于下列命题:
,对于下列命题: ;
;  对称;
对称;  .
.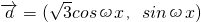 ,
,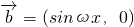 ,其中
,其中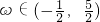 ,函数
,函数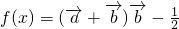 ,且f(x)的图象关于直线
,且f(x)的图象关于直线 对称.
对称. 个单位,再将得到的图象的横坐标变为原来的2倍(纵坐标不变)后得到的y=g(x)的图象;若函数y=g(x),
个单位,再将得到的图象的横坐标变为原来的2倍(纵坐标不变)后得到的y=g(x)的图象;若函数y=g(x),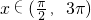 的图象与y=a的图象有三个交点且交点的横坐标成等比数列,求a的值.
的图象与y=a的图象有三个交点且交点的横坐标成等比数列,求a的值.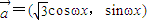 ,
,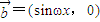 ,其中
,其中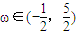 ,函数
,函数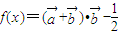 ,且f(x)的图象关于直线
,且f(x)的图象关于直线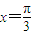 对称.
对称.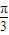 个单位,再将得到的图象的横坐标变为原来的2倍(纵坐标不变)后得到的y=g(x)的图象;若函数y=g(x),
个单位,再将得到的图象的横坐标变为原来的2倍(纵坐标不变)后得到的y=g(x)的图象;若函数y=g(x),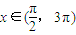 的图象与y=a的图象有三个交点且交点的横坐标成等比数列,求a的值.
的图象与y=a的图象有三个交点且交点的横坐标成等比数列,求a的值.