题目内容
二项式![]() 的展开式中所有有理项的系数和等于 .(用数字作答)
的展开式中所有有理项的系数和等于 .(用数字作答)
考点:
二项式系数的性质.
专题:
计算题.
分析:
利用二项展开式的通项公式Tr+1=![]() •(2)4﹣r•(﹣1)r•
•(2)4﹣r•(﹣1)r•![]() ,(r=0,1,…4)可求得展开式中所有有理项,继而可求得答案.
,(r=0,1,…4)可求得展开式中所有有理项,继而可求得答案.
解答:
解:∵Tr+1=![]() •24﹣r•(﹣1)r•
•24﹣r•(﹣1)r•![]() ,(r=0,1,…4)
,(r=0,1,…4)
∴r=0,2,4时,Tr+1=![]() •24﹣r•(﹣1)r•
•24﹣r•(﹣1)r•![]() 为有理项,
为有理项,
∴二项式![]() 的展开式中所有有理项的系数和等于:
的展开式中所有有理项的系数和等于:
![]() •24+
•24+![]() •22+
•22+![]() =16+24+1=41.
=16+24+1=41.
故答案为:41.
点评:
本题考查二项展开式的通项公式,考查思维分析与运算能力,属于中档题.

练习册系列答案
相关题目
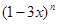 的展开式中所有项的系数之和等于64,那么这个展开式中含x2项的系数是_______.
的展开式中所有项的系数之和等于64,那么这个展开式中含x2项的系数是_______. 的展开式中所有项的二项式系数之和是64,则展开式中含x3项的系数是 .
的展开式中所有项的二项式系数之和是64,则展开式中含x3项的系数是 . 的展开式中所有二项式系数的和为32,且此二项展开式中x10项的系数为a,则
的展开式中所有二项式系数的和为32,且此二项展开式中x10项的系数为a,则 的值为 .
的值为 .