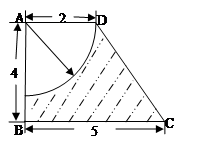题目内容
如图,正三棱柱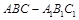 中,侧面
中,侧面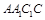 是边长为2的正方形,
是边长为2的正方形,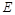 是
是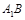 的中点,
的中点,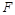 在棱
在棱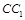 上.
上.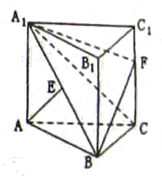
(1)当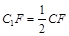 时,求三棱锥
时,求三棱锥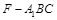 的体积.
的体积.
(2)当点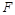 使得
使得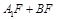 最小时,判断直线
最小时,判断直线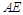 与
与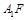 是否垂直,并证明结论.
是否垂直,并证明结论.
(1)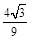 ,(2)垂直,利用线面垂直证明线线垂直
,(2)垂直,利用线面垂直证明线线垂直
解析试题分析:(1)因为侧面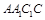 是边长为2的正方形,
是边长为2的正方形,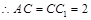
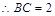
又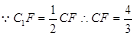
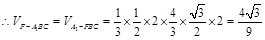
(2)解法1:将侧面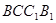 展开到侧面
展开到侧面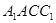 得到矩形
得到矩形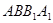 ,连结
,连结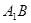 ,交
,交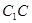 于点
于点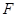 ,此时点
,此时点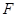 使得
使得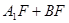 最小.此时
最小.此时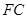 平行且等于
平行且等于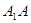 的一半,
的一半,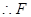 为
为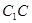 的中点.连接
的中点.连接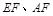
在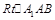 中,
中,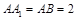 得
得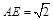
在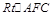 中,
中,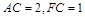 得
得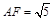
在等腰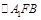 中,
中,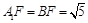 得
得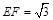
所以由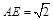 ,
,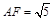 ,
,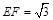 得
得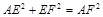 有勾股定理知
有勾股定理知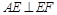
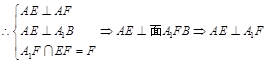
解法2:将侧面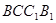 展开到侧面
展开到侧面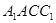 得到矩形
得到矩形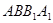 ,连结
,连结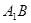 ,交
,交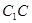 于点
于点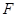 ,此时点
,此时点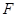 使得
使得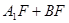 最小.此时
最小.此时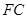 平行且等于
平行且等于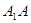 的一半,
的一半,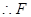 为
为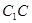 的中点.过点
的中点.过点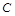 作
作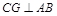 交
交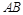 于
于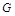 ,连接
,连接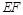 ,由
,由 且
且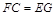 知四边形
知四边形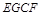 为
为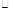 所以
所以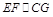 .在正三棱柱
.在正三棱柱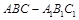 中知
中知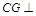 面
面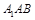 ,而
,而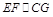 ,所以
,所以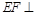 面
面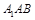 .
.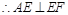
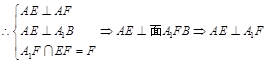
考点:本题考查了空间中的线面关系及体积的计算
点评:以棱锥为载体考查立体几何中的线面、面面、点面位置关系或体积是高考的亮点,掌握其判定性质及定理,是解决此类问题的关键

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
相关题目
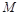 是
是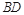 的中点.又已知侧视图是直角梯形,俯视图是等腰直角三角形,有关数据如图所示.
的中点.又已知侧视图是直角梯形,俯视图是等腰直角三角形,有关数据如图所示.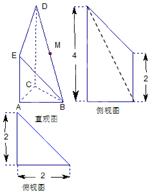
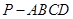 中,
中,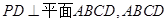 是正方形,E是
是正方形,E是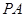 的中点,
的中点,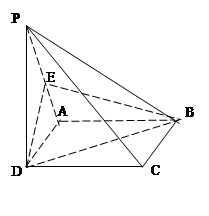
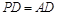 ,求 PC与面AC所成的角
,求 PC与面AC所成的角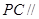 平面
平面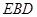
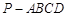 中
中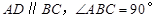 ,
,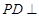 平面
平面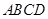 ,
,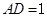 ,
,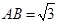 ,
,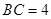 .
.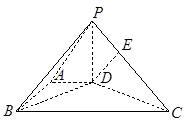
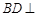
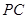 ;
;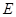 在棱
在棱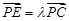 ,若
,若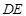 ∥平面
∥平面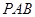 ,求
,求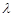 的值.
的值.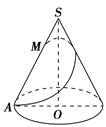
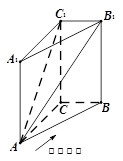
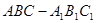 的三视图和直观图如图所示.
的三视图和直观图如图所示.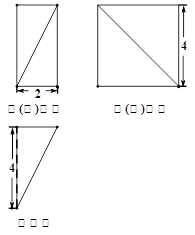
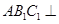 平面
平面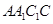 ;
;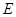 是线段
是线段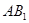 上的一点,且满足
上的一点,且满足 ,求
,求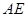 的长.
的长.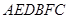 的直观图及三视图如图所示,
的直观图及三视图如图所示, 分别为
分别为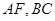 的中点.
的中点.
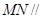 平面
平面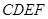 ;
;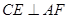 ;
;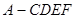 的体积。
的体积。 为梯形,
为梯形, ,
,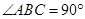 ,求图中阴影部分绕
,求图中阴影部分绕 旋转一周所形成的几何体的表面积和体积。
旋转一周所形成的几何体的表面积和体积。