题目内容
求由直线x=1,x=2,y=0及曲线y=
分析:利用求曲边梯形面积的步骤逐步求解.
解:(1)分割
在区间[1,2]内等间隔地插入n-1个点,将它等分成n个小区间:[1,![]() ],[
],[![]() ,
,![]() ],…,[
],…,[![]() ,2],记第i个区间为[
,2],记第i个区间为[![]() ](i=1,2,…,n),其长度为Δx=
](i=1,2,…,n),其长度为Δx=![]()
分别过上述n-1个点作x轴的垂线,把曲边梯形分成n个小曲边梯形(如下图),它们的面积记作ΔS1,ΔS2,…,ΔSn.
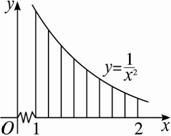
则小曲边梯形面积的和为S=![]() .
.
(2)近似代替
记f(x)=![]() ,当n很大,即Δx很小时,在区间
,当n很大,即Δx很小时,在区间![]() 上,可以认为f(x)=
上,可以认为f(x)=![]() 的值变化很小,近似地等于一个常数,不妨认为它等于
的值变化很小,近似地等于一个常数,不妨认为它等于![]() .从图形上看,就是用平行于x轴的直线段近似地代替小曲边梯形的曲边.这样,在区间
.从图形上看,就是用平行于x轴的直线段近似地代替小曲边梯形的曲边.这样,在区间![]() 上,用小矩形面积ΔSi′近似地代替ΔSi,即在局部小范围内“以直代曲”,则有ΔSi≈ΔSi′=f
上,用小矩形面积ΔSi′近似地代替ΔSi,即在局部小范围内“以直代曲”,则有ΔSi≈ΔSi′=f![]() (i=1,2,…,n).
(i=1,2,…,n).
(3)求和
小曲边梯形的面积和Sn=![]()
![]()
![]()
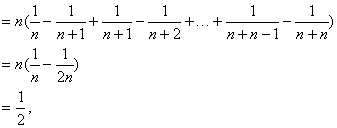
从而得到S的近似值S=Sn≈![]()
(4)取极限
分别将区间[1,2]等分成8,16,20,…等份时,Sn越来越趋向于S,当n趋向于+∞时,Sn无限趋近于![]() .
.
由此可知图形面积为![]() .
.
绿色通道:本题主要考查曲边梯形面积的求解方法.用分割、近似代替、求和、取极限这四个步骤可以求曲边多边形的面积,它体现了一种化整(分割)为零,积零为整(逼近)的思想方法.

练习册系列答案
相关题目
 为曲线
为曲线 在点(1,0)处的切线,直线
在点(1,0)处的切线,直线 为该曲线的另一条切线,且
为该曲线的另一条切线,且