题目内容
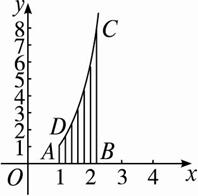
求由直线x=1,x=2和y=0及曲线y=x3围成的图形的面积.
解:(1)分割
如图,把曲边梯形ABCD分割成n个小曲边梯形,用分点![]() 把区间[1,2]等分成n个小区间:[1,
把区间[1,2]等分成n个小区间:[1,![]() ],[
],[![]() ],…,[
],…,[![]() ],…,[
],…,[![]() ],每个小区间的长度为Δx=
],每个小区间的长度为Δx=![]() ,过各分点作x轴的垂线,把曲边梯形ABCD分割成n个小曲边梯形,它们的面积分别记作ΔS1,ΔS2,…,ΔSn.
,过各分点作x轴的垂线,把曲边梯形ABCD分割成n个小曲边梯形,它们的面积分别记作ΔS1,ΔS2,…,ΔSn.
(2)近似代替取各小区间的左端点ξi,用以点ξi的纵坐标ξi3为一边,以小区间长Δx=![]() 为其邻边的小矩形面积近似代替第i个小曲边梯形面积,可以近似地表示为
为其邻边的小矩形面积近似代替第i个小曲边梯形面积,可以近似地表示为
ΔSi≈ξi3·Δx=![]() (i=1,2,3,…,n).
(i=1,2,3,…,n).
(3)求和
因为每一个小矩形的面积都可以作为相应的小曲边梯形面积的近似值,所以n个小矩形面积的和就是曲边梯形ABCD面积S的近似值,即
![]() ①
①
(4)求极限
当分点数目愈多,即Δx愈小时,和式①的值就愈接近曲边梯形ABCD的面积S.因此,n→∞即Δx→0时,和式①的极限就是所求的曲边梯形ABCD的面积.
∵![]()
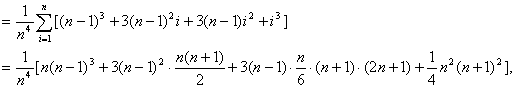
∴![]()

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
 为曲线
为曲线 在点(1,0)处的切线,直线
在点(1,0)处的切线,直线 为该曲线的另一条切线,且
为该曲线的另一条切线,且