题目内容
2．原点在圆C：x2+y2+2y+a-2=0外，则a的取值范围是（ ）| A． | a＞2 | B． | 2＜a＜3 | C． | a＜2 | D． | 0＜a＜2 |
分析 根据二次方程表示圆的条件，以及圆心到原点的距离大于半径，列出不等式组，综合可得实数a的取值范围．
解答 解：∵圆x2+y2+2y+a-2=0，即x2+（y+1）2=3-a，
∴3-a＞0，即a＜3．
∵原点（0，0）在圆x2+y2+2y+a-2=0的外部，∴a-2＞0，∴a＞2．
综上可得，2＜a＜3，
故选：B．
点评 本题主要考查圆的标准方程、点和圆的位置关系，属于基础题．
练习册系列答案
赢在课堂名师课时计划系列答案
天天向上课时同步训练系列答案
阳光课堂同步练习系列答案
相关题目
12．设集合A={1，2，3，5}，B={2，4，6}，则A∩B=（ ）
| A． | {2} | B． | {4，6} | C． | {1，3，5} | D． | {4，6，7，8} |
13．为了得到函数=4sin（2x+$\frac{π}{5}$），x∈R的图象，只需把函数y=4sin（x+$\frac{π}{5}$），x∈R的图象上所有点的（ ）
| A． | 横坐标伸长到原来的2倍，纵坐标不变 | |
| B． | 纵坐标伸长到原来的2倍，横坐标不变 | |
| C． | 横坐标缩短到原来的$\frac{1}{2}$倍，纵坐标不变 | |
| D． | 纵坐标缩短到原来的$\frac{1}{2}$倍，横坐标不变 |
10．下列函数中，既不是奇函数，也不是偶函数的是（ ）
| A． | y=x+sin2x | B． | y=2x+$\frac{1}{{2}^{x}}$ | C． | y=x2+sinx | D． | y=x2-cosx |
17．已知函数f（x）是定义在R上的奇函数，且在区间[0，+∞）上单调递增，若$\frac{{|f（lnx）-f（ln\frac{1}{x}）|}}{2}＞f（1）$，则x的取值范围是（ ）
| A． | $（-∞\;，\;\;\frac{1}{e}）$ | B． | （e，+∞） | C． | $（\frac{1}{e}\;，\;\;e）$ | D． | $（0\;，\;\;\frac{1}{e}）$∪（e，+∞） |
7．已知向量$\overrightarrow{a}$=（sinθ，1），$\overrightarrow{b}$=（2cosθ，-1），且θ∈（0，π），若$\overrightarrow{a}⊥\overrightarrow{b}$，则θ=（ ）
| A． | $\frac{π}{6}$ | B． | $\frac{π}{4}$ | C． | $\frac{π}{2}$ | D． | $\frac{3π}{4}$ |
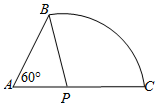某柱体实心铜制零件的截面边长是长度为55毫米线段AB和88毫米的线段AC以及圆心为P，半径为PB的一段圆弧BC构成，其中∠BAC=60°．