Question

某种汽车，购车费用是10万元，每年使用的保险费、养路费、汽油费为0.9万元，年维修费第一年是0.2万元，以后逐年递增0.2万元.问这种汽车使用多少年时，它的平均费用最少？

Answer 1

思路分析：年平均费用等于总费用除以年数，总费用包括：购车费用、保险费、养路费、汽油费以及维修费用的总和，因此，应先计算总费用，列出函数关系，再计算年平均费用.

解：设使用x年时平均费用最少.

由于“年维修费第一年是0.2万元，以后逐年递增0.2万元”,可知汽车每年维修费构成以0.2万元为首项，0.2万元为公差的等差数列.

因此，汽车使用x年时总的维修费用为x万元.

设汽车的年平均费用为y万元，则有

y=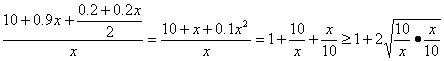=3.

当且仅当，即x=10时，y取最小值.

答：汽车使用10年时平均费用最少.

方法归纳

    在应用平均值不等式解决实际问题时，要注意以下几点：（1）先理解题意，再设变量，设变量时一般把要求最值的变量定为函数；（2）建立相应的函数关系式，把实际问题抽象为函数的最值问题;（3）在定义域内，求出函数的最值；（4）正确写出答案；（5）在特殊情况下，还要根据条件构造满足不等式所要求的条件的结论.