Question

求过三点O(0,0),M₁(1,1),M₂(4,2)的圆的方程,并求圆的半径长和圆心坐标.

Answer 1

解:方法一：设所求圆的方程为x²+y²+Dx+Ey+F=0,由O,M₁,M₂在圆上,则有

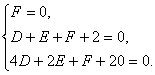解得D=-8,E=6,F=0.

故所求圆的方程为x²+y²-8x+6y=0,即(x－4)²＋(y+3)²=5².

所以圆心坐标为(4,-3),半径为5.

方法二：先求出OM₁的中点E(,),M₁M₂的中点F(,),

再写出OM₁的垂直平分线PE的直线方程y=-(x),①

AB的垂直平分线PF的直线方程y=-3(x),②

联立①②得解得则点P的坐标为(4,-3),即为圆心.OP=5为半径.

方法三：设所求圆的圆心坐标为P(a,b),根据圆的性质可得|OP|=|AP|=|BP|,

即x²+y²=(x-1)²+(y-1)²=(x-4)²+(y-2)²,

解之,得P(4,-3),OP=5为半径.

方法四：设所求圆的方程为(x－a)²＋(y－b)²=r²,因为O(0,0)、A(1,1)、B(4,2)在圆上,所以它们的坐标是方程的解.把它们的坐标代入上面的方程,可以得到关于a、b、r的方程组,即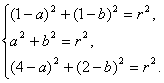解此方程组得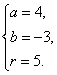

所以所求圆的方程为(x－4)²＋(y+3)²=5²,圆心坐标为(4,-3),半径为5.

点评：请同学们比较,关于何时设圆的标准方程,何时设圆的一般方程.一般说来,如果由已知条件容易求圆心的坐标、半径或需要用圆心的坐标、半径列方程的问题,往往设圆的标准方程；如果已知条件和圆心坐标或半径都无直接关系,往往设圆的一般方程.