题目内容
如图,四棱锥P-ABCD的底面ABCD是边长为2的菱形,∠BAD=60°,已知PB=PD=2,PA=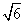 .
.
(1)证明:PC⊥BD;
(2)若E为PA的中点,求三棱锥P-BCE的体积.

解析: (1)证明:连接AC,交BD于点O,连接PO.
因为底面ABCD是菱形,所以AC⊥BD,BO=DO.
由PB=PD知,PO⊥BD.
又因为PO∩AC=O,所以BD⊥平面APC.
又PC⊂平面APC,因此BD⊥PC.

(2)因为E是PA的中点,
所以V三棱锥P-BCE=V三棱锥C-PEB
=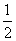 V三棱锥C-PAB
V三棱锥C-PAB
=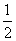 V三棱锥B-APC.
V三棱锥B-APC.
由PB=PD=AB=AD=2知,△ABD≌△PBD.
因为∠BAD=60°,
所以PO=AO=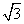 ,AC=2
,AC=2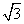 ,BO=1.
,BO=1.
又PA=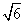 ,所以PO2+AO2=PA2,所以PO⊥AC,
,所以PO2+AO2=PA2,所以PO⊥AC,
故S△APC=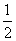 PO·AC=3.
PO·AC=3.
由(1)知,BO⊥平面APC,
因此V三棱锥P-BCE=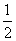 V三棱锥B-APC=
V三棱锥B-APC=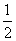 ·
·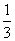 ·BO·S△APC=
·BO·S△APC=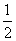 .
.

练习册系列答案
相关题目
总体由编号为01,02,…,19,20的20个个体组成,利用下面的随机数表选取5个个体,选取方法是从随机数表第1行的第5列和第6列数字开始由左到右依次选取两个数字,则选出来的第5个个体的编号为( )
| 7816 6572 0802 6314 0702 4369 9728 0198 |
| 3204 9234 4935 8200 3623 4869 6938 7481 |
A.08 B.07
C.02 D.01
 =a+bi(a、b∈R),则a+b=________.
=a+bi(a、b∈R),则a+b=________. ,
, =2
=2 ,求点M、N及
,求点M、N及 的坐标.
的坐标.
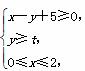 围成的三角形区域内有一个内切圆,向该三角形区域内随机投一个点,该点落在圆内的概率是关于t的函数P(t),则( )
围成的三角形区域内有一个内切圆,向该三角形区域内随机投一个点,该点落在圆内的概率是关于t的函数P(t),则( )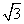 b,则角A等于( )
b,则角A等于( ) B.
B. 
 D.
D. 
 ,求证:a>b.
,求证:a>b.