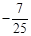题目内容
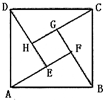 2002年8月,在北京召开的国际数学家大会会标如图所示,它是由4个相同的直角三角形与中间的小正方形拼成的一大正方形,若直角三角形中较大的锐角为θ,大正方形的面积是1,小正方形的面积是
2002年8月,在北京召开的国际数学家大会会标如图所示,它是由4个相同的直角三角形与中间的小正方形拼成的一大正方形,若直角三角形中较大的锐角为θ,大正方形的面积是1,小正方形的面积是| 1 | 25 |
分析:设较大的锐角∠ABF为θ,根据大正方形的面积求出边长AB,由小正方形的面积求出边长EF,在直角三角形ABF中,根据锐角三角形函数定义表示出AF和FB,由大正方形面积减去小正方形得到四个直角三角形的面积,即可求出直角三角形ABF的面积,而三角形ABF的面积可以用直角边AF和FB乘积的一半来求出,两种方法求出的面积相等,列出关系式,根据二倍角的正弦函数公式化简,得到sin2θ的值,利用万能公式得出关于tanθ的方程,求出方程的解即可得到tanθ的值.
解答:解:如图,由已知得:∠ABF=θ,(
<θ<
),AB=1,EF=
,
∴AF=AB•sinθ=sinθ,BF=AB•cosθ=cosθ,(6分)
∵S△ABF=
(S正方形ABCD-S正方形EFGH)=
(1-
)=
,
且S△ABF=
AF•BF=
sinθcosθ,
∴
sinθcosθ=
,
∴sin2θ=
=
,
化简得:12tan2θ-25tanθ+12=0,
解得:tanθ=
或tanθ=
(θ为较大的锐角,不合题意,舍去)(10分)
∴tanθ=
.(12分)
| π |
| 4 |
| π |
| 2 |
| 1 |
| 5 |
∴AF=AB•sinθ=sinθ,BF=AB•cosθ=cosθ,(6分)
∵S△ABF=
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 25 |
| 6 |
| 25 |
且S△ABF=
| 1 |
| 2 |
| 1 |
| 2 |
∴
| 1 |
| 2 |
| 6 |
| 25 |
∴sin2θ=
| 24 |
| 25 |
| 2tanθ |
| 1+tan2θ |
化简得:12tan2θ-25tanθ+12=0,
解得:tanθ=
| 4 |
| 3 |
| 3 |
| 4 |
∴tanθ=
| 4 |
| 3 |
点评:此题考查了锐角函数定义,二倍角的正弦函数公式,以及万能公式,本题的思路为:借助图形,根据题意得出直角三角形ABF的面积,进而得到sin2θ的值,利用万能公式得到关于tanθ的方程,可求出tanθ的值,同时根据θ为较大的锐角,得到tanθ的值大于1,舍去不合题意的tanθ的值.

练习册系列答案
相关题目
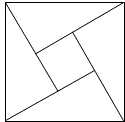 2002年8月,在北京召开的国际数学家大会会标如图所示,它是由4个相同的直角三角形与中间的小正方形拼成的一个大正方形,若直角三角形中较小的锐角为θ,大正方形的面积是1,小正方形的面积是
2002年8月,在北京召开的国际数学家大会会标如图所示,它是由4个相同的直角三角形与中间的小正方形拼成的一个大正方形,若直角三角形中较小的锐角为θ,大正方形的面积是1,小正方形的面积是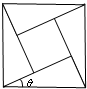 2002年8月,在北京召开国际数学家大会,大会会标如图所示,它是由四个相同的直角三角形、与中间的小正方形拼成的大正方形.若直角三角形中较小的锐角为θ,大正方形的面积为1,小正方形的面积为
2002年8月,在北京召开国际数学家大会,大会会标如图所示,它是由四个相同的直角三角形、与中间的小正方形拼成的大正方形.若直角三角形中较小的锐角为θ,大正方形的面积为1,小正方形的面积为 2002年8月,在北京召开的国际数学家大会会标如图所示,它是由4个相同的直角三角形与中间的小
2002年8月,在北京召开的国际数学家大会会标如图所示,它是由4个相同的直角三角形与中间的小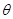 ,大正方形的面积是1,小正方形的面积是
,大正方形的面积是1,小正方形的面积是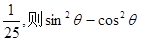 的值等于( )
的值等于( )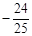 C.
C.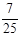 D.
D.