题目内容
数列{an}的各项均为正数，Sn为其前n项和，对于任意n∈N*，总有an，Sn，an2成等差数列．
（1）求数列{an}的通项公式；
（2）设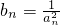
，数列{bn}的前n项和为Tn，求证：
．
解：（1）由已知：对于n∈N*，总有2Sn=an+an2①成立
∴
（n≥2）②
①-②得2an=an+an2-an-1-an-12，∴an+an-1=（an+an-1）（an-an-1）
∵an，an-1均为正数，∴an-an-1=1（n≥2）∴数列{an}是公差为1的等差数列
又n=1时，2S1=a1+a12，解得a1=1，∴an=n．（n∈N*）
（2）解：由（1）可知
∵
∴
分析：（1）根据an=Sn-Sn-1，整理得an-an-1=1（n≥2）进而可判断出数列{an}是公差为1的等差数列，根据等差数列的通项公式求得答案．
（2）由（1）知，因为，所以
，从而得证．
点评：本题主要考查了等差数列的通项公式和等差数列的性质，考查放缩法．从而综合考查了学生分析问题的能力．
∴
（n≥2）②①-②得2an=an+an2-an-1-an-12，∴an+an-1=（an+an-1）（an-an-1）
∵an，an-1均为正数，∴an-an-1=1（n≥2）∴数列{an}是公差为1的等差数列
又n=1时，2S1=a1+a12，解得a1=1，∴an=n．（n∈N*）
（2）解：由（1）可知
∵∴
分析：（1）根据an=Sn-Sn-1，整理得an-an-1=1（n≥2）进而可判断出数列{an}是公差为1的等差数列，根据等差数列的通项公式求得答案．
（2）由（1）知
，因为，所以，从而得证．点评：本题主要考查了等差数列的通项公式和等差数列的性质，考查放缩法．从而综合考查了学生分析问题的能力．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目