题目内容
有三个球,第一个球内切于正方体的六个面,第二个球与这个正方体各条棱相切,第三个球过这个正方体的各个顶点,求这三个球的表面积之比.
解:设正方体的棱长为a,

(1)正方体的内切球球心是正方体的中心,切点是六个面的中心,经过四个切点及球心作截面如图①,
所以有2r1=a,r1= ,所以
,所以 ;
;
(2)球与正方体各棱的切点在每条棱的中点,过球心作正方体的对角面得截面如图②,
 ,所以
,所以 ;
;
(3)正方体的各个顶点在球面上,过球心作正方体的对角面得截面如图③,
所以有 ,所以
,所以 ;
;
由上知: 。
。

(1)正方体的内切球球心是正方体的中心,切点是六个面的中心,经过四个切点及球心作截面如图①,
所以有2r1=a,r1=
 ,所以
,所以 ;
;(2)球与正方体各棱的切点在每条棱的中点,过球心作正方体的对角面得截面如图②,
 ,所以
,所以 ;
;(3)正方体的各个顶点在球面上,过球心作正方体的对角面得截面如图③,
所以有
 ,所以
,所以 ;
;由上知:
 。
。 
练习册系列答案
相关题目
有三个球,第一个球内切于正方体的六个面,第二个球与这个正方体的各条棱都相切,第三个球过这个正方体的各顶点,这三个球的表面积之比为
[
]|
A .1∶2∶3 |
B .1∶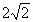 ∶ ∶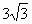 |
|
C .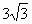 ∶ ∶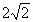 :1 :1 |
D .1∶4∶9 |
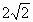 ∶
∶