题目内容
设函数f（x）=x-xlnx．
（Ⅰ）求f（x）的单调区间；
（Ⅱ）若方程f（x）=t在
上有两个实数解，求实数t的取值范围．
解：（Ⅰ）f′（x）=1-（lnx+1）=-lnx，
令f′（x）＞0，得0＜x＜1，令f′（x）＜0，得x＞1，
∴f（x）的增区间为（0，1]，减区间为[1，+∞）．
（Ⅱ）由（Ⅰ）知：当x=1时，f（x）取得极大值为1，
f（
）=
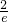，f（e）=0，
由函数f（x）=x-xlnx与f（x）=t的图象知
实数t的取值范围为[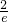，1）．
分析：（Ⅰ）对函数求导，（xlnx）′=（x）′lnx+x（lnx）′，（lnx）′=
，分别令导数大于0，小于0，得x的取值区间，即为f（x）的单调区间；
（Ⅱ）由（Ⅰ）知，f（x）的单调性，求出极大值，求出区间两个端点的函数值，利用两个函数的图象可得实数t的取值范围．
点评：本题考查了利用导数求函数的单调区间，知函数图象的大致走向，注意把方程解的个数问题转化为对应函数图象的交点个数问题，可使问题直观易懂．
令f′（x）＞0，得0＜x＜1，令f′（x）＜0，得x＞1，
∴f（x）的增区间为（0，1]，减区间为[1，+∞）．
（Ⅱ）由（Ⅰ）知：当x=1时，f（x）取得极大值为1，
f（
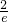）=，f（e）=0，由函数f（x）=x-xlnx与f（x）=t的图象知
实数t的取值范围为[
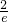，1）．分析：（Ⅰ）对函数求导，（xlnx）′=（x）′lnx+x（lnx）′，（lnx）′=
，分别令导数大于0，小于0，得x的取值区间，即为f（x）的单调区间；（Ⅱ）由（Ⅰ）知，f（x）的单调性，求出极大值，求出区间两个端点的函数值，利用两个函数的图象可得实数t的取值范围．
点评：本题考查了利用导数求函数的单调区间，知函数图象的大致走向，注意把方程解的个数问题转化为对应函数图象的交点个数问题，可使问题直观易懂．
练习册系列答案
相关题目
设函数f（x）的定义域为A，若存在非零实数t，使得对于任意x∈C（C⊆A），有x+t∈A，且f（x+t）≤f（x），则称f（x）为C上的t低调函数．如果定义域为[0，+∞）的函数f（x）=-|x-m2|+m2，且 f（x）为[0，+∞）上的10低调函数，那么实数m的取值范围是（ ）
| A、[-5，5] | ||||||||
B、[-
| ||||||||
C、[-
| ||||||||
D、[-
|