题目内容
已知直线L：y=ax+2和A（1，4），B（3，1）两点，当直线L与线段AB相交时，求实数a的取值范围．分析：本题考查的知识点是斜率的定义及范围，处理的方法是：①由直线L：y=ax+2的方程，判断L恒过P（0，2）点，②求出KPA与KPB③判断过P点的竖直直线与AB两点的关系④写出满足条件的直线斜率的取值范围．
解答：解：由直线L：y=ax+2可得
直线L衡过（0，2）点，如下图示：
∵KPA=2，KPB=-
故a∈[-
，2]
直线L衡过（0，2）点，如下图示：
∵KPA=2，KPB=-
| 1 |
| 3 |
故a∈[-
| 1 |
| 3 |
点评：
求衡过P点且与线段AB相交的直线的斜率的取值范围，有两种情况：
当AB，在P竖直方向上的同侧时，（如本题）计算KPA与KPB，若KPA＜KPB，则直线的斜率k∈[KPA，KPB]
当AB，在P竖直方向上的异侧时，（如下图）计算KPA与KPB，若KPA＜KPB，则直线的斜率k∈（-∞，KPA]∪[KPB，+∞）
求衡过P点且与线段AB相交的直线的斜率的取值范围，有两种情况：当AB，在P竖直方向上的同侧时，（如本题）计算KPA与KPB，若KPA＜KPB，则直线的斜率k∈[KPA，KPB]
当AB，在P竖直方向上的异侧时，（如下图）计算KPA与KPB，若KPA＜KPB，则直线的斜率k∈（-∞，KPA]∪[KPB，+∞）
练习册系列答案
相关题目
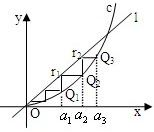设a＞0，如图，已知直线l：y=ax及曲线C：y=x2，C上的点Q1的横坐标为a1（0＜a1＜a）．从C上的点Qn（n≥1）作直线平行于x轴，交直线l于点Pn+1，再从点Pn+1作直线平行于y轴，交曲线C于点Qn+1．Qn（n=1，2，3，…）的横坐标构成数列{an}．