题目内容
在平面直角坐标系![]() 中,动点
中,动点![]() 到定点
到定点![]() 的距离比它到
的距离比它到![]() 轴的距离大
轴的距离大![]() ,设动点
,设动点![]() 的轨迹是曲线
的轨迹是曲线![]() .
.
(1)求曲线![]() 的轨迹方程;
的轨迹方程;
(2) 设直线![]() :
:![]() 与曲线
与曲线![]() 相交于
相交于![]() 、
、![]() 两点,已知圆
两点,已知圆![]() 经过原点
经过原点![]() 和
和![]() 两点,求圆
两点,求圆![]() 的方程,并判断点
的方程,并判断点![]() 关于直线
关于直线![]() 的对称点
的对称点![]() 是否在圆
是否在圆![]() 上.
上.
【解析】(1)由已知,即动点![]() 到定点
到定点![]() 的距离等于它到定直线
的距离等于它到定直线![]() 的距离,∴动点
的距离,∴动点![]() 的轨迹曲线
的轨迹曲线![]() 是顶点在原点,焦点为
是顶点在原点,焦点为![]() 的抛物线和点
的抛物线和点![]()
∴曲线![]() 的轨迹方程为
的轨迹方程为![]() 和
和![]() .
.
(2)由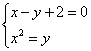 解得
解得![]() 或
或![]()
即![]() ,
,![]()
设过原点与点![]() 、
、![]() 的圆
的圆![]() 的方程为
的方程为![]() ,
,
则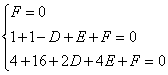 ,解得
,解得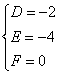
∴圆![]() 的方程为
的方程为![]() 即
即![]()
由上可知,过点![]() 且与直线
且与直线![]() 垂直的直线
垂直的直线![]() 方程为:
方程为:![]()
解方程组![]() ,得
,得![]()
即线段![]() 中点坐标为
中点坐标为![]()
从而易得点![]() 关于直线
关于直线![]() 的对称点
的对称点![]() 的坐标为
的坐标为![]()
把代入![]() 代入:
代入:![]()
∴点![]() 不在圆
不在圆![]() 上.
上.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案
相关题目