题目内容
椭圆
+y2=1的内接矩形的面积的最大值为 .
| x2 | 4 |
分析:由题意的方程可知:矩形的对角线的斜率存在.设椭圆内接矩形一条对角线的方程为y=kx,不妨设k>0.
与椭圆的方程联立距离解得第一象限的顶点A(x,y),再利用内接矩形的面积S=2x•2y=4xy,及基本不等式即可得出.
与椭圆的方程联立距离解得第一象限的顶点A(x,y),再利用内接矩形的面积S=2x•2y=4xy,及基本不等式即可得出.
解答:解:由题意的方程可知:矩形的对角线的斜率存在.
设椭圆内接矩形一条对角线的方程为y=kx,不妨设k>0.
联立
,
化为(1+4k2)x2=4,取第一象限的顶点A(x,y),
解得x=
,∴y=
.
∴内接矩形的面积S=2x•2y=4xy=4×
=
≤
=4.当且仅当k=
上取等号.
故椭圆
+y2=1的内接矩形的面积的最大值为4.
故答案为:4.
设椭圆内接矩形一条对角线的方程为y=kx,不妨设k>0.
联立
|
化为(1+4k2)x2=4,取第一象限的顶点A(x,y),
解得x=
| 2 | ||
|
| 2k | ||
|
∴内接矩形的面积S=2x•2y=4xy=4×
| 4k |
| 1+4k2 |
| 16 | ||
|
| 16 | ||||
2
|
| 1 |
| 2 |
故椭圆
| x2 |
| 4 |
故答案为:4.
点评:本题考查了椭圆的对称性、内接矩形的面积的最大值问题、基本不等式的性质,属于难题.

练习册系列答案
相关题目
椭圆
+y2=1的两个焦点为F1、F2,过F1作垂直于x轴的直线与椭圆相交,一个交点为P,则P到F2的距离为( )
| x2 |
| 4 |
A、
| ||||
B、
| ||||
C、
| ||||
| D、4 |
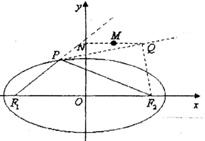 如图,已知椭圆
如图,已知椭圆