题目内容
已知点A,B的坐标分别是(-1,0),(1,0),直线AM,BM相交于点M,且直线AM与直线BM的斜率之差是2,则点M的轨迹方程是
- A.x2=-(y-1)
- B.x2=-(y-1)(x≠±1)
- C.xy=x2-1
- D.xy=x2-1(x≠±1)
B
分析:设M(x,y),先表示直线AM、BM的斜率,再利用斜率之差可得所求方程.
解答:设M(x,y),则kBM=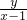 (x≠1),kAM=
(x≠1),kAM= (x≠-1),
(x≠-1),
直线AM与直线BM的斜率之差是2,
所以kAM-kBM=2,
 =2,(x≠±1),
=2,(x≠±1),
整理得x2+y-1=0 (x≠±1).
故选B.
点评:本题主要考查轨迹方程的求法,考查计算能力,注意斜率存在的条件.属于中档题.
分析:设M(x,y),先表示直线AM、BM的斜率,再利用斜率之差可得所求方程.
解答:设M(x,y),则kBM=
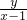 (x≠1),kAM=
(x≠1),kAM= (x≠-1),
(x≠-1),直线AM与直线BM的斜率之差是2,
所以kAM-kBM=2,
 =2,(x≠±1),
=2,(x≠±1),整理得x2+y-1=0 (x≠±1).
故选B.
点评:本题主要考查轨迹方程的求法,考查计算能力,注意斜率存在的条件.属于中档题.

练习册系列答案
相关题目