题目内容
已知函数
(1)求函数 的最小值及单调减区间;
的最小值及单调减区间;
(2)在
 中,
中, 分别是角
分别是角 的对边,且
的对边,且 ,
, ,
, ,且
,且 ,求
,求 ,c的值
,c的值

(1)求函数
 的最小值及单调减区间;
的最小值及单调减区间;(2)在

 中,
中, 分别是角
分别是角 的对边,且
的对边,且 ,
, ,
, ,且
,且 ,求
,求 ,c的值
,c的值(1)最小值为-1,单调减区间为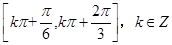 ;(2)
;(2)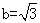 ,
, 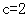
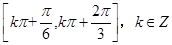 ;(2)
;(2)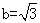 ,
, 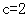
试题分析:(1)因为已知函数
 通过化一公式函数
通过化一公式函数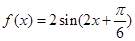 .又因为函数
.又因为函数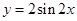 的单调递减区间是
的单调递减区间是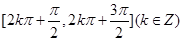 .所以可得
.所以可得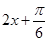 在该区间内的范围即可求得
在该区间内的范围即可求得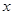 的范围.
的范围.(2)因为在

 中,
中, 分别是角
分别是角 的对边,且
的对边,且 由(1)式可求得角A的值.再利用余弦定理即可得可求得三角形中的边
由(1)式可求得角A的值.再利用余弦定理即可得可求得三角形中的边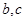 的关系.从而即可求出
的关系.从而即可求出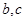 的值.
的值.试题解析:(1)

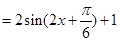
∴函数
 的最小值为
的最小值为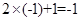
由
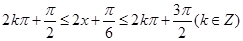 得:
得:单调减区间为
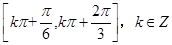 6分
6分(2)
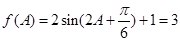
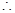
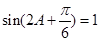
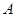 是三角形内角,∴
是三角形内角,∴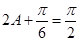
即
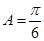
∴
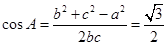 即:
即: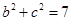 .
. 将
 代入可得:
代入可得: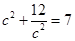 ,解之得:
,解之得: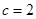 或
或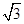 .
.∴,
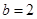 或
或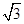
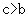 , ∴
, ∴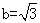 ,
, 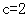 , 13分
, 13分 
练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
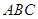 的内角
的内角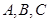 所对边的长分别为
所对边的长分别为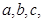 ,且有
,且有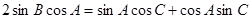 .
.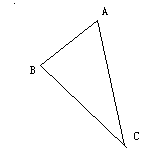
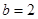 ,
,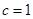 ,
,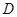 为
为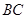 的中点,求
的中点,求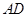 的长.
的长. ,-1),n=(cos A,sin A).若m⊥n,且acos C+ccos A=bsin B,则角C的大小为________.
,-1),n=(cos A,sin A).若m⊥n,且acos C+ccos A=bsin B,则角C的大小为________. ,点D在BC边上,∠ADC=75°,则AD的长为________.
,点D在BC边上,∠ADC=75°,则AD的长为________.
 中,
中, ,
, ,则
,则 的最小值为 .
的最小值为 . 中,记角
中,记角 、
、 、
、 所对的边分别为
所对的边分别为 、
、 、
、 ,且这三角形的三边长是公差为1的等差数列,若最小边
,且这三角形的三边长是公差为1的等差数列,若最小边 ,则
,则 ( ).
( ).



 中,若
中,若 则角
则角 .
. 中,若
中,若 ,
, ,
, ,则三角形
,则三角形 的面积
的面积 ________.
________. 中,若
中,若 ,则
,则 边上的高等于 .
边上的高等于 .