题目内容
设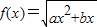 .
.(1)当a=-1,b=4时,求函数f(ex)(e是自然对数的底数.)的定义域和值域;
(2)求满足下列条件的实数a的值:至少有一个正实数b,使函数f(x)的定义域和值域相同.
【答案】分析:(1)先求出函数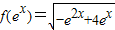 ,结合函数解析式可得-e2x+4ex≥0,解不等式可求函数的定义域
,结合函数解析式可得-e2x+4ex≥0,解不等式可求函数的定义域
利用换元法,结合二次函数的性质可求函数的值域
(2)结合函数解析式的特点,考虑对a分类讨论:对①a=0,②a>0,③a<0三种情况分别求解函数的值域,即可进行判断
解答:(14分)解:(1)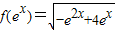 ,
,
由-e2x+4ex≥0解得0<ex≤4,∴x≤ln4,
所以函数f(ex)的定义域是(-∞,ln4].…(2分)
设ex=t>0,则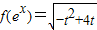 ,
,
记g(t)=-t2+4t(t>0),∴g(t)∈[0,4],∴f(ex)∈[0,2],即f(ex)的值域是[0,2]…(4分)
(2)①若a=0,则对于每个正数b,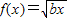 的定义域和值域都是[0,+∞)
的定义域和值域都是[0,+∞)
故a=0满足条件; …(6分)
②若a>0,则对于正数b,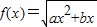 的定义域为D={x|ax2+bx≥0}=
的定义域为D={x|ax2+bx≥0}=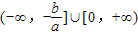 ,
,
但f(x)的值域A⊆[0,+∞),
故D≠A,即a>0不合条件; …(9分)
③若a<0,则对正数b,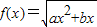 的定义域
的定义域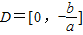
由于此时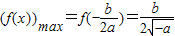 ,故f(x)的值域为
,故f(x)的值域为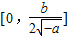
则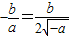
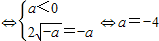
综上所述:a的值为0或-4…(14分)
点评:本题主要考查了换元法求解函数的值域,二次函数性质的应用,值域的求解,体现了分类讨论思想的应用
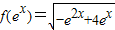 ,结合函数解析式可得-e2x+4ex≥0,解不等式可求函数的定义域
,结合函数解析式可得-e2x+4ex≥0,解不等式可求函数的定义域利用换元法,结合二次函数的性质可求函数的值域
(2)结合函数解析式的特点,考虑对a分类讨论:对①a=0,②a>0,③a<0三种情况分别求解函数的值域,即可进行判断
解答:(14分)解:(1)
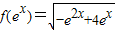 ,
,由-e2x+4ex≥0解得0<ex≤4,∴x≤ln4,
所以函数f(ex)的定义域是(-∞,ln4].…(2分)
设ex=t>0,则
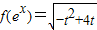 ,
,记g(t)=-t2+4t(t>0),∴g(t)∈[0,4],∴f(ex)∈[0,2],即f(ex)的值域是[0,2]…(4分)
(2)①若a=0,则对于每个正数b,
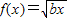 的定义域和值域都是[0,+∞)
的定义域和值域都是[0,+∞)故a=0满足条件; …(6分)
②若a>0,则对于正数b,
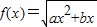 的定义域为D={x|ax2+bx≥0}=
的定义域为D={x|ax2+bx≥0}=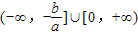 ,
,但f(x)的值域A⊆[0,+∞),
故D≠A,即a>0不合条件; …(9分)
③若a<0,则对正数b,
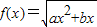 的定义域
的定义域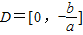
由于此时
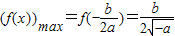 ,故f(x)的值域为
,故f(x)的值域为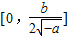
则
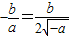
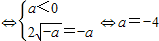
综上所述:a的值为0或-4…(14分)
点评:本题主要考查了换元法求解函数的值域,二次函数性质的应用,值域的求解,体现了分类讨论思想的应用

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目