题目内容
椭圆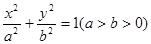 的两焦点为
的两焦点为 、
、 ,以
,以 为边作正三角形,若椭圆恰好平分该正三角形的另两边,则椭圆的离心率是( )
为边作正三角形,若椭圆恰好平分该正三角形的另两边,则椭圆的离心率是( )
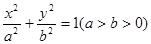 的两焦点为
的两焦点为 、
、 ,以
,以 为边作正三角形,若椭圆恰好平分该正三角形的另两边,则椭圆的离心率是( )
为边作正三角形,若椭圆恰好平分该正三角形的另两边,则椭圆的离心率是( )A. | B. | C. | D. |
D
试题分析:以
 为边作正三角形,则三角形的第三个顶点一定在y轴上,又因为椭圆恰好平分该正三角形的另两边,所以另外两边的中点在椭圆上,因为
为边作正三角形,则三角形的第三个顶点一定在y轴上,又因为椭圆恰好平分该正三角形的另两边,所以另外两边的中点在椭圆上,因为 ,不妨设第三个顶点在y轴的正半轴上,则第三个顶点的坐标为
,不妨设第三个顶点在y轴的正半轴上,则第三个顶点的坐标为 ,所以中点
,所以中点 在椭圆上,代入椭圆方程得:
在椭圆上,代入椭圆方程得: ,又因为
,又因为 ,可以得到离心率为
,可以得到离心率为 .
.点评:求椭圆的离心率,只要把
 求出来就可以了,不必把
求出来就可以了,不必把 分别求出来.
分别求出来.
练习册系列答案
相关题目
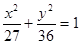 有相同焦点,且经过点
有相同焦点,且经过点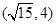 ,
,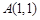 是椭圆
是椭圆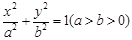 上一点,
上一点,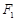 ,
,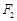 是椭圆的两焦点,且满足
是椭圆的两焦点,且满足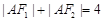
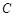 、
、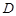 是椭圆上任两点,且直线
是椭圆上任两点,且直线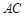 、
、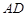 的斜率分别为
的斜率分别为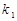 、
、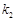 ,若存在常数
,若存在常数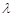 使
使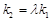 ,求直线
,求直线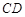 的斜率.
的斜率. 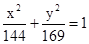 有共同焦点,且过点(0,2)的双曲线方程,并且求出这条双曲线的实轴长、焦距、离心率以及渐近线方程.
有共同焦点,且过点(0,2)的双曲线方程,并且求出这条双曲线的实轴长、焦距、离心率以及渐近线方程.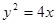 ,焦点为
,焦点为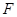 ,顶点为
,顶点为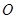 ,点
,点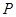 在抛物线上移动,
在抛物线上移动,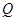 是
是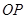 的中点,
的中点,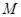 是
是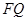 的中点,求点
的中点,求点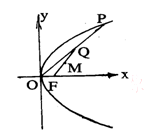
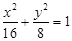 的焦点分别为
的焦点分别为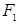 、
、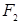 ,以原点为圆心且过焦点的圆O与椭圆相交于点
,以原点为圆心且过焦点的圆O与椭圆相交于点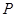 ,则
,则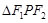 的面积等于( )
的面积等于( )



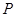 是圆
是圆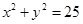 上的动点,点D是
上的动点,点D是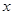 轴上的投影,M为
轴上的投影,M为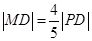
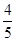 的直线被C所截线段的长度。
的直线被C所截线段的长度。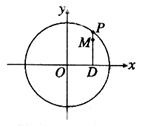
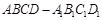 的棱长为
的棱长为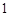 ,点
,点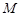 在棱
在棱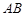 上, 且
上, 且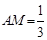 , 点
, 点 是平面
是平面 上的动点,且动点
上的动点,且动点 的距离与点
的距离与点
 , 则以M(4,1)为中点的弦所在直线l的方程是 .
, 则以M(4,1)为中点的弦所在直线l的方程是 .