题目内容
选修4-5:不等式选讲
已知关于x的不等式|2x+1|-|x-1|≤log2a(其中a>0).
(1)当a=4时,求不等式的解集;
(2)若不等式有解,求实数a的取值范围.
解:(Ⅰ)当a=4时,不等式即|2x+1|-|x-1|≤2,当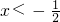 时,不等式为-x-2≤2,解得
时,不等式为-x-2≤2,解得 .(1分)
.(1分)
当 时,不等式为 3x≤2,解得
时,不等式为 3x≤2,解得 .(2分) 当x>1时,不等式为x+2≤2,此时x不存在.(3分)
.(2分) 当x>1时,不等式为x+2≤2,此时x不存在.(3分)
综上,不等式的解集为 .(5分)
.(5分)
(Ⅱ)设f(x)=|2x+1|-|x-1|= ,
,
故 ,即f(x)的最小值为
,即f(x)的最小值为 .(8分)
.(8分)
所以,当f(x)≤log2a有解,则有 ,解得
,解得 ,即a的取值范围是
,即a的取值范围是 .(10分)
.(10分)
分析:(Ⅰ)当a=4时,不等式即|2x+1|-|x-1|≤2,分类讨论,去掉绝对值,分别求出解集,再取并集,即得所求.
(Ⅱ)化简f(x)=|2x+1|-|x-1|的解析式,求出f(x)的最小值为 ,则由
,则由  ,解得实数a的取值范围.
,解得实数a的取值范围.
点评:本题主要考查绝对值不等式的解法,关键是去掉绝对值,化为与之等价的不等式组来解,体现了分类讨论的数学思想,属于中档题.
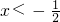 时,不等式为-x-2≤2,解得
时,不等式为-x-2≤2,解得 .(1分)
.(1分)当
 时,不等式为 3x≤2,解得
时,不等式为 3x≤2,解得 .(2分) 当x>1时,不等式为x+2≤2,此时x不存在.(3分)
.(2分) 当x>1时,不等式为x+2≤2,此时x不存在.(3分)综上,不等式的解集为
 .(5分)
.(5分)(Ⅱ)设f(x)=|2x+1|-|x-1|=
 ,
,故
 ,即f(x)的最小值为
,即f(x)的最小值为 .(8分)
.(8分)所以,当f(x)≤log2a有解,则有
 ,解得
,解得 ,即a的取值范围是
,即a的取值范围是 .(10分)
.(10分)分析:(Ⅰ)当a=4时,不等式即|2x+1|-|x-1|≤2,分类讨论,去掉绝对值,分别求出解集,再取并集,即得所求.
(Ⅱ)化简f(x)=|2x+1|-|x-1|的解析式,求出f(x)的最小值为
 ,则由
,则由  ,解得实数a的取值范围.
,解得实数a的取值范围.点评:本题主要考查绝对值不等式的解法,关键是去掉绝对值,化为与之等价的不等式组来解,体现了分类讨论的数学思想,属于中档题.

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目