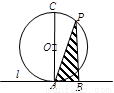题目内容
如图，圆O的直径AC=8cm，直线l与圆相切于点A，P为圆的右半圆弧上的动点，PB⊥直线l于B，求△PAB面积的最大值．
【答案】分析：以直线l所在的直线为x轴，以AC所在的直线为y轴，建立平面直角坐标系，可得圆的方程为 x2+（y-4）2=16，（0＜y＜8）．设△PAB面积为S，则
S2=
x2•y2=2y3-
y4．利用导数求得S2的最大值，从而求得S的最大值．
解答：解：以直线l所在的直线为x轴，以AC所在的直线为y轴，建立平面直角坐标系，
则圆心O为（0，4），且半径为4，
圆的方程为 x2+（y-4）2=16，（0＜y＜8）．
故△PAB面积为S=
•AB•BP=
xy，∴S2=
x2•y2=
[16-（y-4）2]y2=2y3-
y4．
由于函数S2的导数为 （S2）′=6y2-y3，令 （S2）′=6y2-y3=0，可得y=6，
故当y=6时，S2取得最大值为108，故S的最大值为6
（平方厘米）．
点评：本题主要考查求圆的标准方程，利用导数求函数的最值，属于中档题．
S2=
x2•y2=2y3-y4．利用导数求得S2的最大值，从而求得S的最大值．解答：解：以直线l所在的直线为x轴，以AC所在的直线为y轴，建立平面直角坐标系，
则圆心O为（0，4），且半径为4，
圆的方程为 x2+（y-4）2=16，（0＜y＜8）．
故△PAB面积为S=
•AB•BP=xy，∴S2=x2•y2=[16-（y-4）2]y2=2y3-y4．由于函数S2的导数为 （S2）′=6y2-y3，令 （S2）′=6y2-y3=0，可得y=6，
故当y=6时，S2取得最大值为108，故S的最大值为6
（平方厘米）．点评：本题主要考查求圆的标准方程，利用导数求函数的最值，属于中档题．
练习册系列答案
互动课堂系列答案
激活思维智能训练课时导学练系列答案
相关题目
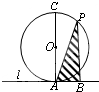如图，圆O的直径AC=8cm，直线l与圆相切于点A，P为圆的右半圆弧上的动点，PB⊥直线l于B，求△PAB面积的最大值．
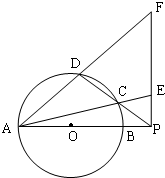（2012•许昌三模）如图，圆O的直径AB=d，P是AB延长线上一点，Bp=a，割线PCD交圆O于点C、D，过点P作AP的垂线，交直线AC于点E，交直线AD于点F．
