题目内容
已知函数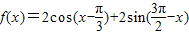
（1）求函数f（x）的单调递减区间．
（2）求函数f（x）的最大值，并求f（x）取得最大值时的x的集合．
（3）若
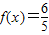，求
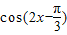的值．
【答案】分析：由题意可得：f（x）=2sin（x-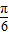
）．（1）当
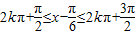，即化简可得函数的单调减区间．（2）根据正弦函数的性质可得：当
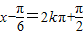，即
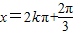时，函数f（x）有最大值．（3）由题意可得：2sin（x-
）=
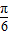，所以sin（x-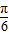
）=
．再集合二倍角公式可得：cos（2x-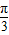
）=1-2sin2（x-
）=
．
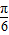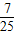解答：解：由题意可得：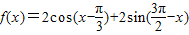
，化简可得f（x）=2sin（x-
）．
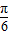（1）当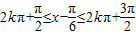
，即化简可得
，
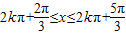所以函数f（x）的单调递减区间为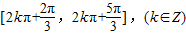
．
（2）当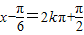
，即
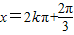时，函数f（x）有最大值，
并且此时x的集合为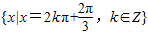
．
（3）由题意可得：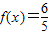
，即2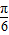sin（x-
）=
，所以sin（x-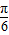
）=
．
所以cos（2x-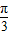
）=1-2sin2（x-
）=
．
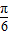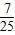点评：解决此类问题的关键是熟练掌握两角和与差的正弦余弦公式，以及三角函数的有关性质．
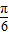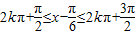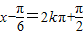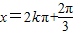）．（1）当，即化简可得函数的单调减区间．（2）根据正弦函数的性质可得：当，即时，函数f（x）有最大值．（3）由题意可得：2sin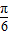（x-）=，所以sin（x-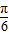）=．再集合二倍角公式可得：cos（2x-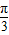）=1-2sin2（x-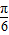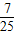）=．解答：解：由题意可得：
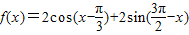，化简可得f（x）=2sin（x-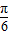）．（1）当
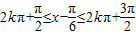，即化简可得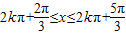，所以函数f（x）的单调递减区间为
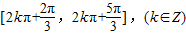．（2）当
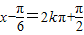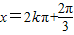，即时，函数f（x）有最大值，并且此时x的集合为
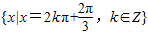．（3）由题意可得：
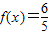，即2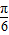sin（x-）=，所以sin（x-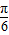）=．所以cos（2x-
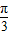）=1-2sin2（x-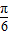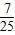）=．点评：解决此类问题的关键是熟练掌握两角和与差的正弦余弦公式，以及三角函数的有关性质．
练习册系列答案
名师点拨卷系列答案
英才计划期末调研系列答案
相关题目
（1）求函数
在区间[1，
]上的最大值、最小值；
）上，函数
图象的下方；
，求证：
≥
。（
）
的极值点；
过点（0，—1），并且与曲线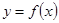
相切，求直线
，其中
，求函数
在
上的最小值.（其中e为自然对数的底数）