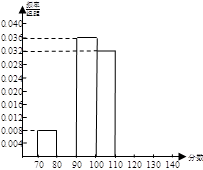题目内容
某学生社团在对本校学生学习方法开展问卷调查的过程中发现,在回收上来的1000份有效问卷中,同学们背英语单词的时间安排共有两种:白天背和晚上临睡前背。为研究背单词时间安排对记忆效果的影响,该社团以5%的比例对这1000名学生按时间安排类型进行分层抽样,并完成一项实验,实验方法是,使两组学生记忆40个无意义音节(如XIQ、GEH),均要求在刚能全部记清时就停止识记,并在8小时后进行记忆测验。不同的是,甲组同学识记结束后一直不睡觉,8小时后测验;乙组同学识记停止后立刻睡觉,8小时后叫醒测验。
两组同学识记停止8小时后的准确回忆(保持)情况如图(区间含左端点而不含右端点)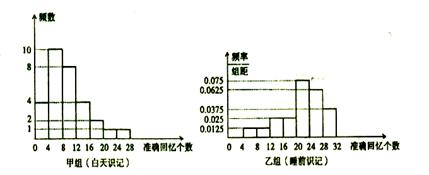
(1)估计1000名被调查的学生中识记停止后8小时40个音节的保持率大于等于60%的人数;
(2)从乙组准确回忆因结束在[12,24)范围内的学生中随机选3人,记能准确回忆20个以上(含20)的人数为随机变量X,求X分布列及数学期望;
(3)从本次实验的结果来看,上述两种时间安排方法中哪种方法背英语单词记忆效果更好? 计算并说明理由。
(Ⅰ)即估计1000名被调查的学生中识记停止8小时后40个音节的保持率大于等于60%的人数为180人.
(Ⅱ) 的分布列为
的分布列为
0 1 2 3 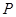




数学期望 .
.
(Ⅲ)乙组学生平均保持率为 ,
,
所以临睡前背单词记忆效果更好.
解析试题分析:(Ⅰ)∵ ,
,
由甲图知,甲组有 (人),∴乙组有20人.
(人),∴乙组有20人.
又∵ ,
,
∴识记停止8小时后40个音节的保持率大于等于60%的在甲组中有1人
乙组有 (人)
(人)
∴
即估计1000名被调查的学生中识记停止8小时后40个音节的保持率大于等于60%的人数为180人.
(Ⅱ)由乙图知,乙组在 之间有
之间有 (人)
(人)
在 之间有
之间有 (人)
(人)
∴ 的可能取值为0,1,2,3
的可能取值为0,1,2,3
 ,
, ,
, ,
,

∴ 的分布列为
的分布列为
数学期望
0 1 2 3 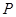




 .
. 
(Ⅲ)参考答案:
甲组学生准确回忆音节数共有: 个
个
故甲组学生的平均保持率为
乙组学生准确回忆音节数共有: 个
个
故乙组学生平均保持率为 ,
,
所以临睡前背单词记忆效果更好. (只要叙述合理都给分)
(只要叙述合理都给分)
考点:本题主要考查频率分布直方图,频率的概念及计算,随机变量的分布列与期望。
点评:典型题,统计中的抽样方法,频率直方图,概率计算及分布列问题,是高考必考内容及题型。题中随机变量分布列的确定思路明确。计算概率时,注意准确计算组合数。对计算能力要求较高。

有甲、乙两个班级进行数学考试,按照大于或等于85分为优秀,85分以下为非优秀统计成绩后,得到如下的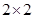 列联表:已知从全部210人中随机抽取1人为优秀的概率为
列联表:已知从全部210人中随机抽取1人为优秀的概率为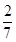 .
.
| | 优秀 | 非优秀 | 总计 |
| 甲班 | 20 | | |
| 乙班 | | 60 | |
| 合计 | | | 210 |
(Ⅰ)请完成上面的
 列联表,并判断若按99%的可靠性要求,能否认为“成绩与班级有关”;
列联表,并判断若按99%的可靠性要求,能否认为“成绩与班级有关”;(Ⅱ)从全部210人中有放回抽取3次,每次抽取1人,记被抽取的3人中的优秀人数为
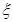 ,若每次抽取的结果是相互独立的,求
,若每次抽取的结果是相互独立的,求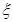 的分布列及数学期望
的分布列及数学期望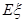 .
.
假设关于某设备使用年限x(年)和所支出的维修费用y(万元)有如下统计资料:若由资料知,y对x呈线性相关关系,试求:
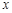 | 2 | 3 | 4 | 5 | 6 |
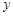 | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
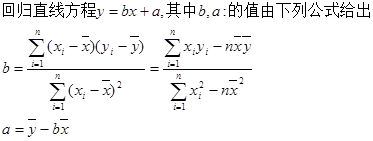 .
. 某高校从参加今年自主招生考试的学生中随机抽取容量为50的学生成绩样本,得频率分布表如下:
| 组号 | 分组 | 频数 | 频率 |
| 第一组 | [230,235) | 8 | 0.16 |
| 第二组 | [235,240) | ① | 0.24 |
| 第三组 | [240,245) | 15 | ② |
| 第四组 | [245,250) | 10 | 0.20 |
| 第五组 | [250,255] | 5 | 0.10 |
| 合 计 | 50 | 1.00 | |
(2)为了选拔出更优秀的学生,高校决定在第三、四、五组中用分层抽样法抽取6名学生进行第二轮考核,分别求第三、四、五各组参加考核人数;
(3)在(2)的前提下,高校决定在这6名学生中录取2名学生,求2人中至少有1名是第四组的概率.
在某次测验中,有6位同学的平均成绩为75分.用 表示编号为
表示编号为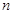
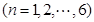 的同学所得成绩,且前5位同学的成绩如下:
的同学所得成绩,且前5位同学的成绩如下:
编号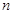 | 1 | 2 | 3 | 4 | 5 |
成绩 | 70 | 76 | 72 | 70 | 72 |
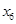 ,及这6位同学成绩的标准差
,及这6位同学成绩的标准差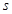 ;
;(2)从前5位同学中,随机地选2位同学,求恰有1位同学成绩在区间(68,75)中的概率.
在某次测验中,有6位同学的平均成绩为75分.用xn表示编号为n(n=1,2, ,6)的同学所得成绩,且前5位同学的成绩如下:
| 编号n | 1 | 2 | 3 | 4 | 5 |
| 成绩xn | 70 | 76 | 72 | 70 | 72 |
(2)从前5位同学中,随机地选2位同学,求恰有1位同学成绩在区间(68,75)中的概率.
某校的研究性学习小组为了研究高中学生的身体发育状况,在该校随机抽出120名17至18周岁的男生,其中偏重的有60人,不偏重的也有60人。在偏重的60人中偏高的有40人,不偏高的有20人;在不偏重的60人中偏高和不偏高人数各占一半
(1)根据以上数据建立一个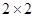 列联表:
列联表:
| | 偏重 | 不偏重 | 合计 |
| 偏高 | | | |
| 不偏高 | | | |
| 合计 | | | |