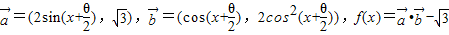题目内容
已知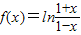
（1）求f（x）的定义域
（2）判断f（x）的奇偶性并证明
（3）求使f（x）＞0的x的取值范围．
【答案】分析：（1）利用对数的真数大于0，解不等式即可求出f（x）的定义域
（2）直接利用函数的奇偶性的定义判断即可．
（3）转化f（x）＞0，利用对数函数的单调性求解不等式即可得到x的取值范围．
解答：解：（1）∵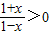
，∴-1＜x＜1
（2）由（1）知函数的定义域关于原点对称
又∵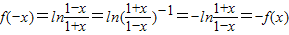
所以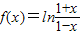
为奇函数
（3）∵f（x）＞0，即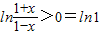
∵以e为底的对数是增函数∴
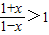，∴0＜x＜1
所以f（x）＞0的x取值范围为{x|0＜x＜1}
点评：本题考查函数的定义域，函数的奇偶性，以及对数函数的单调性的应用，考查计算能力．
（2）直接利用函数的奇偶性的定义判断即可．
（3）转化f（x）＞0，利用对数函数的单调性求解不等式即可得到x的取值范围．
解答：解：（1）∵
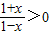，∴-1＜x＜1（2）由（1）知函数的定义域关于原点对称
又∵
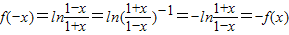
所以
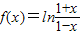为奇函数（3）∵f（x）＞0，即
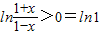∵以e为底的对数是增函数∴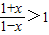，∴0＜x＜1所以f（x）＞0的x取值范围为{x|0＜x＜1}
点评：本题考查函数的定义域，函数的奇偶性，以及对数函数的单调性的应用，考查计算能力．
练习册系列答案
应用题天天练四川大学出版社系列答案
相关题目
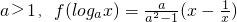
时，f（x）的最小值为2，求f（x）≥2成立的x的取值集合．
的值．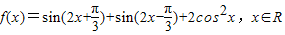
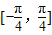上没有零点，求m的取值范围．
