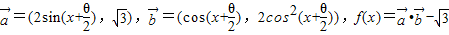题目内容
已知


(1)求f(x)在[0,2π]上的单调区间
(2)当x
 时,f(x)的最小值为2,求f(x)≥2成立的x的取值集合.
时,f(x)的最小值为2,求f(x)≥2成立的x的取值集合.(3)若存在实数a,b,C,使得a[f(x)-m]+b[f(x-C)-m]=1,对任意x∈R恒成立,求
 的值.
的值.
【答案】分析:(1)化简函数f(x)的解析式为2sin(x+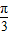 )+1+m 由x∈[0,2π],可得
)+1+m 由x∈[0,2π],可得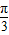 ≤x+
≤x+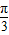 ≤2π+
≤2π+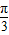 .分
.分 时、
时、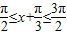 时、
时、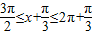 时三种情况,分别求得函数的单调区间.
时三种情况,分别求得函数的单调区间.
(2)根据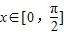 ,求得
,求得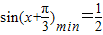 ,可得f(x)min=2+m=2,由此求得m的值.再由f(x)≥2,可得
,可得f(x)min=2+m=2,由此求得m的值.再由f(x)≥2,可得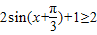
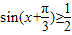 ,
,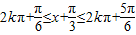 ,由此求得x的集合.
,由此求得x的集合.
(3)由题意可得对任意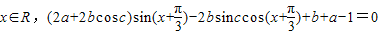 恒成立,故有(2a+2bcosC)=0,且2bsinC=0,且b+a-1=0.由此求得
恒成立,故有(2a+2bcosC)=0,且2bsinC=0,且b+a-1=0.由此求得 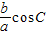 的值.
的值.
解答:解:(1)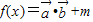 =2sin
=2sin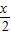 cos
cos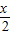 -2
-2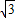
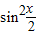 +
+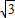 +1+m=sinx+
+1+m=sinx+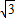 cosx+1+m=2sin(x+
cosx+1+m=2sin(x+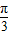 )+1+m
)+1+m
由x∈[0,2π],可得 ≤x+
≤x+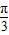 ≤2π+
≤2π+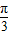 .
.
当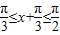 时,可得函数f(x)在
时,可得函数f(x)在 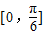 上递增,当
上递增,当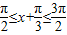 时,可得函数f(x)在
时,可得函数f(x)在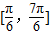 上 递减.
上 递减.
当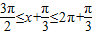 时,可得函数在
时,可得函数在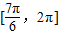 上递增.------------(2分)
上递增.------------(2分)
(2)由于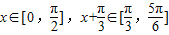 ,故
,故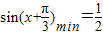 ,所以f(x)min=2+m=2 所以 m=0.--------(1分)
,所以f(x)min=2+m=2 所以 m=0.--------(1分)
所以, ,由f(x)≥2,可得
,由f(x)≥2,可得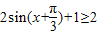
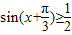 ,
,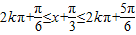 ,
,
所以{x|2kπ-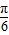 ≤x≤2kπ+
≤x≤2kπ+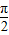 k∈z}.--------(3分)
k∈z}.--------(3分)
(3)∵
=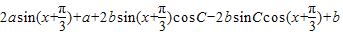 ,
,
对任意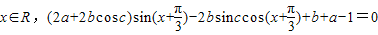 恒成立,
恒成立,
故有(2a+2bcosC)=0,且2bsinC=0,且b+a-1=0.
经讨论只能有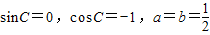 ,所以,
,所以,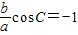 .--------(4分)
.--------(4分)
点评:本题主要考查复合三角函数的单调性,两个向量的数量积的运算,函数的恒成立问题,属于中档题.
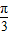 )+1+m 由x∈[0,2π],可得
)+1+m 由x∈[0,2π],可得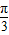 ≤x+
≤x+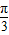 ≤2π+
≤2π+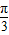 .分
.分 时、
时、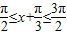 时、
时、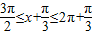 时三种情况,分别求得函数的单调区间.
时三种情况,分别求得函数的单调区间.(2)根据
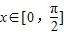 ,求得
,求得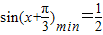 ,可得f(x)min=2+m=2,由此求得m的值.再由f(x)≥2,可得
,可得f(x)min=2+m=2,由此求得m的值.再由f(x)≥2,可得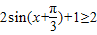
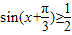 ,
,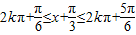 ,由此求得x的集合.
,由此求得x的集合.(3)由题意可得对任意
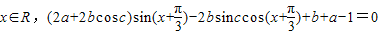 恒成立,故有(2a+2bcosC)=0,且2bsinC=0,且b+a-1=0.由此求得
恒成立,故有(2a+2bcosC)=0,且2bsinC=0,且b+a-1=0.由此求得 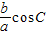 的值.
的值.解答:解:(1)
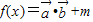 =2sin
=2sin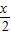 cos
cos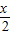 -2
-2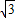
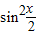 +
+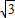 +1+m=sinx+
+1+m=sinx+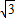 cosx+1+m=2sin(x+
cosx+1+m=2sin(x+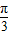 )+1+m
)+1+m 由x∈[0,2π],可得
 ≤x+
≤x+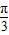 ≤2π+
≤2π+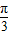 .
.当
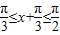 时,可得函数f(x)在
时,可得函数f(x)在 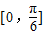 上递增,当
上递增,当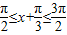 时,可得函数f(x)在
时,可得函数f(x)在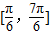 上 递减.
上 递减.当
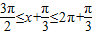 时,可得函数在
时,可得函数在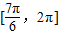 上递增.------------(2分)
上递增.------------(2分)(2)由于
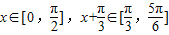 ,故
,故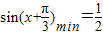 ,所以f(x)min=2+m=2 所以 m=0.--------(1分)
,所以f(x)min=2+m=2 所以 m=0.--------(1分)所以,
 ,由f(x)≥2,可得
,由f(x)≥2,可得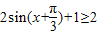
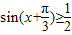 ,
,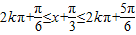 ,
,所以{x|2kπ-
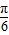 ≤x≤2kπ+
≤x≤2kπ+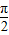 k∈z}.--------(3分)
k∈z}.--------(3分)(3)∵

=
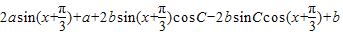 ,
,对任意
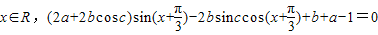 恒成立,
恒成立,故有(2a+2bcosC)=0,且2bsinC=0,且b+a-1=0.
经讨论只能有
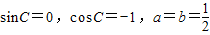 ,所以,
,所以,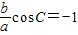 .--------(4分)
.--------(4分)点评:本题主要考查复合三角函数的单调性,两个向量的数量积的运算,函数的恒成立问题,属于中档题.

练习册系列答案
 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案
相关题目
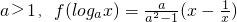
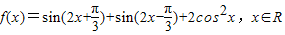
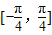 上没有零点,求m的取值范围.
上没有零点,求m的取值范围.