题目内容
正方体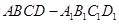 的棱线长为1,面对角线
的棱线长为1,面对角线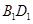 上有两个动点E,F,且
上有两个动点E,F,且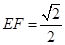 ,则下列四个结论中①
,则下列四个结论中①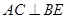 ②
②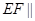 平面
平面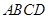 ③三棱锥
③三棱锥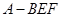 的体积为定值 ④异面直线
的体积为定值 ④异面直线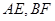 所成的角为定值,其中正确的个数是
所成的角为定值,其中正确的个数是
| A.1 | B.2 | C.3 | D.4 |
C
解析试题分析:①AC⊥BE,由题意及图形知,AC⊥面DD1B1B,故可得出AC⊥BE,此命题正确;
②EF∥平面ABCD,由正方体ABCD-A1B1C1D1的两个底面平行,EF在其一面上,故EF与平面ABCD无公共点,故有EF∥平面ABCD,此命题正确;
③三棱锥A-BEF的体积为定值,由几何体的性质及图形知,三角形BEF的面积是定值,A点到面DD1B1B距离是定值,故可得三棱锥A-BEF的体积为定值,此命题正确;
④异面直线AE、BF所成的角为定值,由图知,当F与B1重合时,令上底面顶点为O,则此时两异面直线所成的角是∠A1AO,当E与D1重合时,此时点F与O重合,则两异面直线所成的角是OBC1,此二角不相等,故异面直线AE、BF所成的角不为定值.
综上知①②③正确,故选C。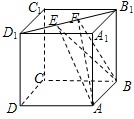
考点:本题主要考查正方体的几何性质。
点评:中档题,解答本题关键是正确理解正方体的几何性质,且能根据这些几何特征,对其中的点线面和位置关系作出正确判断.另外,异面直线所成角的定义以及线面垂直的证明也是解答本题的关键。

已知直线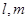 和平面
和平面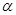 , 则下列命题正确的是
, 则下列命题正确的是
A.若 ∥ ∥ , ,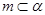 ,则 ,则 ∥ ∥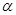 | B.若 ∥ ∥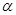 , ,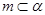 ,则 ,则 ∥ ∥ |
C.若 ⊥ ⊥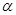 , ,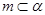 ,则 ,则 ⊥ ⊥ | D.若 ⊥ ⊥ , , ⊥ ⊥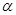 ,则 ,则 ∥ ∥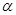 |
已知正方体 中,
中, 、
、 分别为
分别为 、
、 的中点,则异面直线
的中点,则异面直线 与
与 所成角的余弦值为( )
所成角的余弦值为( )
A. | B. | C. | D.0 |
下面四个命题:
①若直线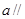 平面
平面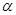 ,则
,则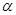 内任何直线都与
内任何直线都与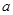 平行;
平行;
②若直线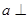 平面
平面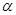 ,则
,则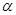 内任何直线都与
内任何直线都与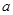 垂直;
垂直;
③若平面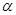
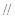 平面
平面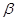 ,则
,则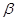 内任何直线都与
内任何直线都与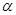 平行;
平行;
④若平面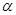
 平面
平面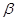 ,则
,则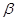 内任何直线都与
内任何直线都与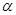 垂直。
垂直。
其中正确的两个命题是( )
| A.①② | B.②③ | C.③④ | D.②④ |
已知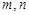 是两条不同直线,
是两条不同直线,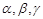 是三个不同平面,下列命题中正确的是( )
是三个不同平面,下列命题中正确的是( )
A.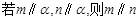 | B.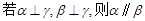 |
C.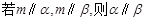 | D.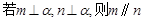 |
若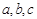 是空间三条不同的直线,
是空间三条不同的直线,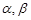 是空间两个不同的平面,则下列命题中,逆命题不正确的是( )
是空间两个不同的平面,则下列命题中,逆命题不正确的是( )
A.当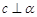 时,若 时,若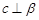 ,则 ,则 |
B.当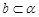 时,若 时,若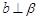 ,则 ,则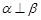 |
C.当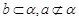 且 且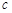 是 是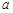 在 在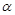 内的射影时,若 内的射影时,若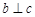 ,则 ,则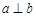 |
D.当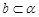 且 且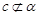 时,若 时,若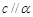 ,则 ,则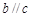 |
在空间,下列命题正确的是( )
| A.平行直线在同一平面内的射影平行或重合 | B.垂直于同一平面的两条直线平行 |
| C.垂直于同一平面的两个平面平行 | D.平行于同一直线的两个平面平行 |
已知m,n为异面直线,m⊥平面α,n⊥平面β,直线l满足l ⊥m,l ⊥n,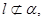 l
l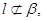 则
则
( )
A.α∥β且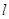 ∥α ∥α | B.α⊥β且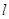 ⊥β ⊥β |
C.α与β相交,且交线垂直于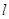 | D.α与β相交,且交线平行于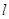 |
 是两个不同的平面,则下列四个命题中是真命题的是( )
是两个不同的平面,则下列四个命题中是真命题的是( )


