题目内容
平面直角坐标系xOy中,已知⊙M经过点F1(0,-c),F2(0,c),A(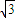 c,0)三点,其中c>0.
c,0)三点,其中c>0.(1)求⊙M的标准方程(用含c的式子表示);
(2)已知椭圆
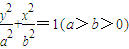 (其中a2-b2=c2)的左、右顶点分别为D、B,⊙M与x轴的两个交点分别为A、C,且A点在B点右侧,C点在D点右侧.
(其中a2-b2=c2)的左、右顶点分别为D、B,⊙M与x轴的两个交点分别为A、C,且A点在B点右侧,C点在D点右侧.①求椭圆离心率的取值范围;
②若A、B、M、O、C、D(O为坐标原点)依次均匀分布在x轴上,问直线MF1与直线DF2的交点是否在一条定直线上?若是,请求出这条定直线的方程;若不是,请说明理由.
【答案】分析:(1)设⊙M的方程为x2+y2+Dx+Ey+F=0,则由题设,得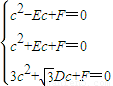 ,由此能求出⊙M的方程.
,由此能求出⊙M的方程.
(2)⊙M与x轴的两个交点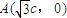 ,
,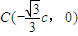 ,又B(b,0),D(-b,0),由题设
,又B(b,0),D(-b,0),由题设 ,由此能求出椭圆离心率的取值范围.
,由此能求出椭圆离心率的取值范围.
(3)由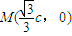 ,得
,得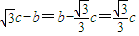 .所以直线MF1的方程为
.所以直线MF1的方程为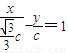 ,由此能够导出直线MF1与直线DF2的交点Q在定直线
,由此能够导出直线MF1与直线DF2的交点Q在定直线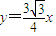 上.
上.
解答:解:(1)设⊙M的方程为x2+y2+Dx+Ey+F=0,
则由题设,得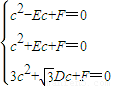
解得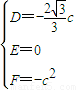
⊙M的方程为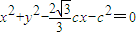 ,
,
⊙M的标准方程为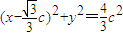 ;(5分)
;(5分)
(2)⊙M与x轴的两个交点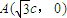 ,
,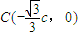 ,
,
又B(b,0),D(-b,0),
由题设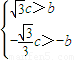 即
即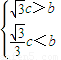
所以 解得
解得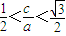 ,
,
即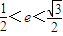 .所以椭圆离心率的取值范围为
.所以椭圆离心率的取值范围为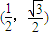 ;(10分)
;(10分)
(3)由(1),得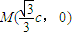 .
.
由题设,得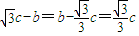 .
.
∴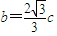 ,
,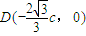 .
.
∴直线MF1的方程为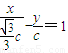 ,
,
①直线DF2的方程为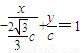 .
.
②由①②,得直线MF1与直线DF2的交点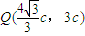 ,
,
易知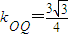 为定值,
为定值,
∴直线MF1与直线DF2的交点Q在定直线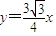 上.(15分)
上.(15分)
点评:本题考查圆锥曲线的性质和应用,解题时要认真审题,仔细解答,注意圆曲线的性质和公式的合理运用.
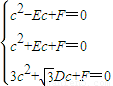 ,由此能求出⊙M的方程.
,由此能求出⊙M的方程.(2)⊙M与x轴的两个交点
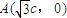 ,
,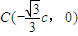 ,又B(b,0),D(-b,0),由题设
,又B(b,0),D(-b,0),由题设 ,由此能求出椭圆离心率的取值范围.
,由此能求出椭圆离心率的取值范围.(3)由
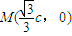 ,得
,得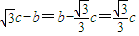 .所以直线MF1的方程为
.所以直线MF1的方程为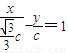 ,由此能够导出直线MF1与直线DF2的交点Q在定直线
,由此能够导出直线MF1与直线DF2的交点Q在定直线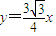 上.
上.解答:解:(1)设⊙M的方程为x2+y2+Dx+Ey+F=0,
则由题设,得
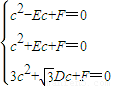
解得
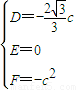
⊙M的方程为
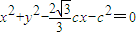 ,
,⊙M的标准方程为
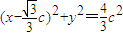 ;(5分)
;(5分)(2)⊙M与x轴的两个交点
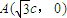 ,
,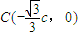 ,
,又B(b,0),D(-b,0),
由题设
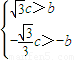 即
即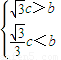
所以
 解得
解得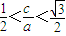 ,
,即
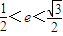 .所以椭圆离心率的取值范围为
.所以椭圆离心率的取值范围为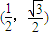 ;(10分)
;(10分)(3)由(1),得
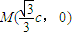 .
.由题设,得
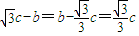 .
.∴
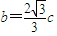 ,
,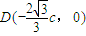 .
.∴直线MF1的方程为
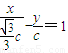 ,
,①直线DF2的方程为
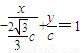 .
.②由①②,得直线MF1与直线DF2的交点
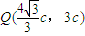 ,
,易知
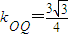 为定值,
为定值,∴直线MF1与直线DF2的交点Q在定直线
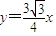 上.(15分)
上.(15分)点评:本题考查圆锥曲线的性质和应用,解题时要认真审题,仔细解答,注意圆曲线的性质和公式的合理运用.

练习册系列答案
相关题目
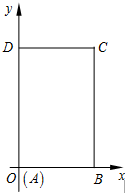 如图,在平面直角坐标系xOy中,已知矩形ABCD的两边AB,CD分别落在x轴、y轴的正半轴上,且AB=2,AD=4,点A与坐标原点重合.现将矩形折叠,使点A落在线段DC上,若折痕所在的直线的斜率为k,试写出折痕所在直线的方程及k的范围.
如图,在平面直角坐标系xOy中,已知矩形ABCD的两边AB,CD分别落在x轴、y轴的正半轴上,且AB=2,AD=4,点A与坐标原点重合.现将矩形折叠,使点A落在线段DC上,若折痕所在的直线的斜率为k,试写出折痕所在直线的方程及k的范围.