Question

已知点P是曲线C：f（x）=e^x+x上的动点，直线l是曲线C在P点处的切线，则直线l倾斜角的取值范围是________．

Answer 1

分析：先根据导数运算对函数 f（x）=e^x+x进行求导，再由切线斜率的值等于该点导函数的值，可求得切线斜率的范围，进而可得到倾斜角α的范围．
解答：∵f（x）=e^x+x，
∴y'=e^x+1，
∴tanα=y'=e^x+1＞1
又∵α∈[0，π），
∴α∈
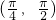
故答案为：．
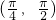点评：本题主要考查函数的求导运算和导数的几何意义．导数是高等数学下放到高中的新内容，是每年高考的热点问题，一定要好好复习．