题目内容
已知向量
=（sinx，cosx），
=（1，-2），且∥，则tanx=________．
-
分析：利用向量共线的坐标形式的公式：坐标交叉相乘其积相等；可列出方程，进而在方程的两边同除以cosx求出tanx．
解答：∵
，
∴-2sinx=cosx．
∴
．
故答案为
．
点评：本题考查向量共线的充要条件：
?x1y2=x2y1；三角函数的商数关系：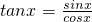
．
分析：利用向量共线的坐标形式的公式：坐标交叉相乘其积相等；可列出方程，进而在方程的两边同除以cosx求出tanx．
解答：∵
，∴-2sinx=cosx．
∴
．故答案为
．点评：本题考查向量共线的充要条件：
?x1y2=x2y1；三角函数的商数关系：．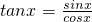 
练习册系列答案
相关题目
已知向量
=（sinx，cosx），向量
=(1，
)，则|
+
|的最大值为（ ）
| a |
| b |
| 3 |
| a |
| b |
| A、3 | ||
B、
| ||
| C、1 | ||
| D、9 |