题目内容
（选修4—5 不等式证明选讲）（本题满分7分）
对于任意实数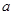
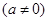和
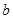，不等式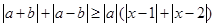
恒成立，试求实数
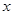的取值范围．
对于任意实数
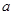
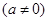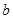和，不等式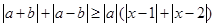恒成立，试求实数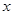的取值范围．
本试题主要是考查了绝对值不等式的恒成立问题的运用。利用绝对值不等式的放缩法，得到参数a分离后的表达式的最值，结合最值得到参数的取值范围的问题。注意利用绝对值不等式的放缩的运用，是解决该试题的关键。
解：由题知，
恒成立，
故
不大于
的最小值 …………3分
∵
，当且仅当
时取等号
∴
的最小值等于2. …………6分
∴x的范围即为不等式|x－1|＋|x－2|≤2的解，解不等式得 ………7分
解：由题知，
恒成立，故
不大于的最小值 …………3分∵
，当且仅当时取等号∴
的最小值等于2. …………6分 ∴x的范围即为不等式|x－1|＋|x－2|≤2的解，解不等式得
………7分
练习册系列答案
数学奥赛暑假天天练南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
是
的一个近似值，令
． 
，求证:
；
比
． 
中至少有一个小于2.
，则实数a的取值范围为 ________． 
则下列不等式正确的是
, 则下列正确的是（ ）
，则
与
的大小关系是____________。
的解集为（ ）。
