题目内容
已知a,b,c∈R,则下列推理其中正确的个数是
① ②
②
③ ④
④ .
.
- A.1
- B.2
- C.3
- D.4
C
分析:利用不等式的基本性质和对数函数的单调性即可判断.
解答:①∵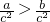 ,∴
,∴ ,∴a>b,故正确;
,∴a>b,故正确;
②∵a3>b3,∴a>b,又ab>0,∴ ,即
,即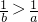 ,故正确;
,故正确;
③取a=-3,b=-2,满足(-3)2>(-2)2,-3×(-2)>0,但是 ,故③不正确;
,故③不正确;
④∵0<a<b<1,∴0>lgb>lga,lg(1-a2)<0,lgalgb>0,lg(1-a)>0,
∴loga(1+a) =
= >
> =
= >0,
>0,
∴ ,故正确.
,故正确.
综上可知:只有①②④正确.
故选C.
点评:熟练掌握不等式的基本性质和对数函数的单调性是解题的关键.
分析:利用不等式的基本性质和对数函数的单调性即可判断.
解答:①∵
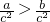 ,∴
,∴ ,∴a>b,故正确;
,∴a>b,故正确;②∵a3>b3,∴a>b,又ab>0,∴
 ,即
,即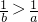 ,故正确;
,故正确;③取a=-3,b=-2,满足(-3)2>(-2)2,-3×(-2)>0,但是
 ,故③不正确;
,故③不正确;④∵0<a<b<1,∴0>lgb>lga,lg(1-a2)<0,lgalgb>0,lg(1-a)>0,
∴loga(1+a)
 =
= >
> =
= >0,
>0,∴
 ,故正确.
,故正确.综上可知:只有①②④正确.
故选C.
点评:熟练掌握不等式的基本性质和对数函数的单调性是解题的关键.

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目