题目内容
已知函数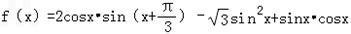 .
.
(1)求函数f(x)的单调递减区间;
(2)将函数f(x)的图象按向量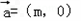 平移,使得平移之后的图象关于直线
平移,使得平移之后的图象关于直线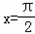 对称,求m的最小正值.
对称,求m的最小正值.
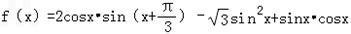 .
.(1)求函数f(x)的单调递减区间;
(2)将函数f(x)的图象按向量
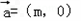 平移,使得平移之后的图象关于直线
平移,使得平移之后的图象关于直线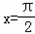 对称,求m的最小正值.
对称,求m的最小正值.(1)f(x)=2cosx( sinx+
sinx+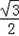 cosx)﹣
cosx)﹣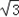 sin2x+sinxcosx
sin2x+sinxcosx
=sinxcosx+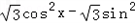 x+sincosx
x+sincosx
=sin2x+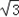 cos2x=2sin(2x+
cos2x=2sin(2x+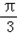 ),
),
由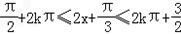 π,k∈Z,
π,k∈Z,
得kπ+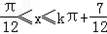 π,k∈Z
π,k∈Z
故函数f(x)的单调递减区间为[kπ+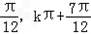 ],k∈Z;
],k∈Z;
(2)由(1)得到函数y=2sin(2x+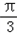 ),
),
此函数按向量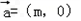 平移得到解析式为y=2sin(2x+
平移得到解析式为y=2sin(2x+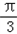 ﹣2m),
﹣2m),
∵y=2sin(2x+ 关于直线x=
关于直线x=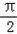 对称,
对称,
∴2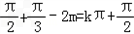 (k∈Z)
(k∈Z)
∴m=﹣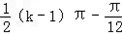 (k∈Z)
(k∈Z)
当k=0时,m的最小正值为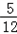 π.
π.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目





 ,如果满足;对任意
,如果满足;对任意 ,存在常数
,存在常数 ,都有
,都有 成立,则称
成立,则称 ,
,
 时,求函数
时,求函数 上的值域,并判断函数
上的值域,并判断函数 上是以3为上界函数值,求实数
上是以3为上界函数值,求实数 的取值范围;
的取值范围; ,求函数
,求函数 在
在 上的上界T的取值范围。
上的上界T的取值范围。 .
. 上的函数值的取值范围.
上的函数值的取值范围. .
. 上的函数值的取值范围.
上的函数值的取值范围.