题目内容

在极坐标系中，曲线C的方程是ρ=2cosθ，过点M(2
2
，
3π
4
)作曲线C的切线，则切线长等于
 
．
分析：先将原极坐标方程是ρ=2cosθ两边同乘以ρ后化成直角坐标方程，点M的坐标化成直角坐标，再利用直角坐标方程结合圆的几何性质进行求解即可．
解答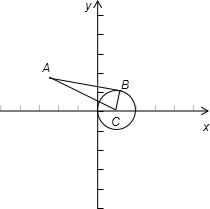：精英家教网解：∵曲线C的直角方程是x2+y2-2x=0，圆心C（1，0），半径BC=1．
点M(2
2
，
3π
4
)的直角坐标是M（-2，2）
如图，在直角三角形ABC中，
切线长AB=
AC2- BC 2
=
(-2-1)2+(2-0)2-12
=2
3
．
故答案为：2
3
．
点评：本题考查点的极坐标和直角坐标的互化，利用直角坐标与极坐标间的关系，即利用ρcosθ=x，ρsinθ=y，ρ2=x2+y2，进行代换即可进行极坐标和直角坐标的互化．
练习册系列答案
相关题目
在极坐标系中，曲线C的极坐标方程为ρ=2
2
sin(θ-
π
4
)，以极点为原点，极轴为x轴的正半轴建立平面直角坐标系，直线l的参数方程为
x=1+
4
5
t
y=-1-
3
5
t
（t为参数），求直线l被曲线C所截得的弦长．
在A、B、C、D四小题中只能选做2题，每小题10分，共计20分，请在答题纸指定区域内作答，解答应写出文字说明、证明过程或演算步骤．
A．选修4-1：（几何证明选讲）
如图，从O外一点P作圆O的两条切线，切点分别为A，B，
AB与OP交于点M，设CD为过点M且不过圆心O的一条弦，
求证：O，C，P，D四点共圆．
B．选修4-2：（矩阵与变换）
已知二阶矩阵M有特征值λ=3及对应的一个特征向量e1=[
 
1
1
]，并且矩阵M对应的变换将点（-1，2）变换成（9，15），求矩阵M．
C．选修4-4：（坐标系与参数方程）
在极坐标系中，曲线C的极坐标方程为p=2
2
sin（θ-
π
4
），以极点为原点，极轴为x轴的正半轴建立平面直角坐标系，直线l的参数方程为
x=1+
4
5
t
y=-1-
3
5
t
（t为参数），求直线l被曲线C所截得的弦长．
D．选修4-5（不等式选讲）
已知实数x，y，z满足x+y+z=2，求2x2+3y2+z2的最小值．
（坐标系与参数方程选做题）在极坐标系中，曲线C的极坐标方程为ρsin（θ-
π
6
）=3，点A（2，
π
3
）到曲线C上点的距离的最小值AP0=
2
2
．
选修4-4：坐标系与参数方程
在极坐标系中，曲线C极坐标方程为ρ=2
2
sin(θ-
π
4
)，以极点为原点，极轴为x轴的正半轴建立平面直角坐标系，直线l的参数方程为
x=1+
4
5
t
y=-1-
3
5
t
（t为参数）．
求：（1）曲线C和直线l的普通方程；
（2）求直线l被曲线C所截得的弦长．
在平面直角坐标系中，已知直线l过点A（2，0），倾斜角为
π2
．
（1）写出直线l的参数方程；
（2）若有一极坐标系分别以直角坐标系的原点和x轴非负半轴为原点和极轴，并且两坐标系的单位长度相等，在极坐标系中有曲线C：ρ2cos2θ=1，求直线l截曲线C所得的弦BC的长度．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网