题目内容
20.已知抛物线$y=\frac{1}{4}{x^2}$和$y=-\frac{1}{16}{x^2}+5$所围成的封闭曲线,给定点A(0,a),若在此封闭曲线上恰有三对不同的点,满足每一对点关于点A对称,则实数a的取值范围是$(\frac{5}{2},4)$.分析 由图可知过两曲线的交点的直线与x轴的交点为(0,4),所以a<4.当对称的两个点分属两段曲线时,设其中一个点为(x1,$\frac{{{x}_{1}}^{2}}{4}$),则其对称点为(-x1,2a-$\frac{{{x}_{1}}^{2}}{4}$),将其代入曲线$y=-\frac{1}{16}{x^2}+5$,得到的关于x1的方程的解有且只有两个,进而可得结果.
解答  解:显然,过点A与x轴平行的直线与封闭曲线的两个交点关于点A对称,且这两个点在同一曲线上.
解:显然,过点A与x轴平行的直线与封闭曲线的两个交点关于点A对称,且这两个点在同一曲线上.
当对称的两个点分属两段曲线时,设其中一个点为(x1,y1),其中y1=$\frac{{{x}_{1}}^{2}}{4}$,且-4≤x1≤4,则其关于点A的对称点为(-x1,2a-y1),
所以这个点在曲线$y=-\frac{1}{16}{x^2}+5$上,
所以2a-y1=-$\frac{1}{16}$x12+5,即2a-$\frac{{{x}_{1}}^{2}}{4}$=-$\frac{1}{16}$x12+5,
所以2a=$\frac{3}{16}$x12+5,即$\frac{3}{16}$x12+5-2a=0,此方程的x1的解必须刚好有且只有两个,
当x1=4时,其对称点的横坐标刚好为-4,故x1≠±4,
于是-4<x1<4,且x1≠0,
∴2a=$\frac{3}{16}$x12+5∈(5,8),即$(\frac{5}{2},4)$.
故答案为:$(\frac{5}{2},4)$.
点评 本题考查点的对称性、一元二次方程根的判别式,属于中档题.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
11.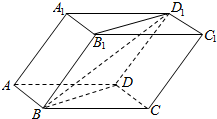 已知斜四棱柱ABCD-A1B1C1D1的各棱长均为2,∠A1AD=60°,∠BAD=90°,平面A1ADD1⊥平面ABCD,则异面直线BD1与AA1所成的角的余弦值为( )
已知斜四棱柱ABCD-A1B1C1D1的各棱长均为2,∠A1AD=60°,∠BAD=90°,平面A1ADD1⊥平面ABCD,则异面直线BD1与AA1所成的角的余弦值为( )
 已知斜四棱柱ABCD-A1B1C1D1的各棱长均为2,∠A1AD=60°,∠BAD=90°,平面A1ADD1⊥平面ABCD,则异面直线BD1与AA1所成的角的余弦值为( )
已知斜四棱柱ABCD-A1B1C1D1的各棱长均为2,∠A1AD=60°,∠BAD=90°,平面A1ADD1⊥平面ABCD,则异面直线BD1与AA1所成的角的余弦值为( )| A. | $\frac{\sqrt{3}}{4}$ | B. | $\frac{\sqrt{13}}{4}$ | C. | $\frac{\sqrt{39}}{13}$ | D. | $\frac{3}{4}$ |
15.已知:对任意x∈[0,1]都有$\sqrt{1-{x^2}}-cosωx≥0$成立,且ω>0则ω的取值范围为( )
| A. | $[\frac{π}{4},\frac{π}{2}]$ | B. | $(\frac{π}{4},\frac{π}{2}]$ | C. | $[\frac{π}{2},\frac{3π}{2}]$ | D. | $[\frac{π}{2},\frac{3π}{2})$ |
5.下列说法错误的是( )
| A. | 自变量取值一定时,因变量的取值带有一定随机性的两个变量之间的关系叫做相关关系 | |
| B. | 在线性回归分析中,相关系数r的值越大,变量间的相关性越强 | |
| C. | 在残差图中,残差点分布的带状区域的宽度越狭窄,其模型拟合的精度越高 | |
| D. | 在回归分析中,R2为0.98的模型比R2为0.80的模型拟合的效果好 |
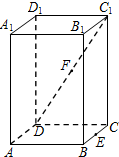 如图,在正四棱柱(底面是正方形的直棱柱)ABCD-A1B1C1D1中,E是BC的中点,F是C1D的中点,P是棱CC1所在直线上的动点.则下列四个命题:
如图,在正四棱柱(底面是正方形的直棱柱)ABCD-A1B1C1D1中,E是BC的中点,F是C1D的中点,P是棱CC1所在直线上的动点.则下列四个命题: