题目内容
已知等比数列 中,
中, 则
则 前3项的和
前3项的和 的取值范围是( )
的取值范围是( )
A. | B. |
C. | D. |
D
解析试题分析:首先由等比数列的通项入手表示出S3(即q的代数式),然后根据q的正负性进行分类,最后利用均值不等式求出S3的范围.
∵等比数列{an}中,a2=1∴S3=a1+a2+a3=a2(1+q+ )=1+q+
)=1+q+ ∴当公比q>0时,S3=1+q+
∴当公比q>0时,S3=1+q+ ≥1+2
≥1+2 =3;当公比q<0时,S3=1-(-q-
=3;当公比q<0时,S3=1-(-q- )≤1-2
)≤1-2 =-1.∴S3∈(-∞,-1]∪[3,+∞).故选D.
=-1.∴S3∈(-∞,-1]∪[3,+∞).故选D.
考点:本试题主要考查了等比数列的通项公式和前n项和的关系式的运用。
点评:解决该试题的关键是利用等比数列的通项公式表示出前3项和,然后借助于第二项得到首项与公比的关系式得到求解。

练习册系列答案
相关题目
各项为正数的等比数列 的公比
的公比 ,且
,且 成等差数列,则
成等差数列,则 的值是( )
的值是( )
A. | B. | C. | D. 或 或 |
已知等比数列 中,各项都是正数,而且
中,各项都是正数,而且 成等差数列,则
成等差数列,则 ( )
( )
A. | B. | C. | D. |
在等比数列 中,
中, (
(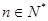 ),
), ,
, ,则
,则 =( )
=( )
A. | B. | C. 或 或 | D. |
记等比数列 的前
的前 项和为
项和为 ,若
,若 则
则 ( )
( )
| A. 9 | B.27 | C. 8 8 | D.8 |
设等比数列 各项均为正数,且
各项均为正数,且 ,则
,则 ( )
( )
| A.1 | B.2 | C.4 | D.0 |
在数列 中,
中, ,其中
,其中 为方程
为方程 的解,则这个数列的前
的解,则这个数列的前 项和
项和 为( )
为( )
A. | B. |
C. | D. |
在等比数列 的值为( )
的值为( )
| A.1 | B.2 | C.3 | D.9 |
 的图象上存在不同的三点到原点的距离构成等比数列,则以下不可能成为该等比数列的公比的数是( )
的图象上存在不同的三点到原点的距离构成等比数列,则以下不可能成为该等比数列的公比的数是( )


