题目内容
如图,已知△AOB,∠AOB= ,∠BAO=
,∠BAO= ,AB=4,D为线段AB的中点,若△AOC是△AOB 绕直线AO旋转而成的,记二面角B-AO-C的大小为θ。
,AB=4,D为线段AB的中点,若△AOC是△AOB 绕直线AO旋转而成的,记二面角B-AO-C的大小为θ。
 ,∠BAO=
,∠BAO= ,AB=4,D为线段AB的中点,若△AOC是△AOB 绕直线AO旋转而成的,记二面角B-AO-C的大小为θ。
,AB=4,D为线段AB的中点,若△AOC是△AOB 绕直线AO旋转而成的,记二面角B-AO-C的大小为θ。
(1)当平面COD⊥平面AOB时,求θ的值;
(2)当 时,求二面角C-OD-B的余弦值的取值范围。
时,求二面角C-OD-B的余弦值的取值范围。
(2)当
 时,求二面角C-OD-B的余弦值的取值范围。
时,求二面角C-OD-B的余弦值的取值范围。| 解:(1)在平面AOB内过B作OD的垂线,垂足为E,如图 因为平面AOB⊥平面COD,平面AOB∩平面COD=OD, 所以BE⊥平面COD, 故BE⊥CO 又因为OC⊥AO, 所以OC⊥平面AOB, 故OC⊥OB 又因为OB⊥OA,OC⊥OA, 所以二面角B-AO-C的平面角为∠COB, 故  。 。(2)当  时,二面角C-OD-B的余弦值为0; 时,二面角C-OD-B的余弦值为0;当  时,过C作OB的垂线,垂足为F, 时,过C作OB的垂线,垂足为F,过F作OD的垂线,垂足为G,连接CG, 则∠CGF的补角为二面角C-OD-B的平面角, 在Rt△OCF中,CF=2sinθ,OF=-2cosθ, 在Rt△CGF中,  所以  因为 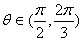 , , 故  所以二面角C-OD-B的余弦值的取值范围为  。 。 |
 |

练习册系列答案
相关题目

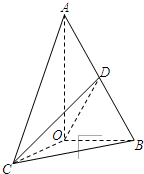 如图,已知△AOB,∠AOB=
如图,已知△AOB,∠AOB=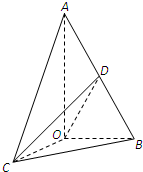 (2011•江西模拟)如图,已知△AOB,∠AOB=
(2011•江西模拟)如图,已知△AOB,∠AOB= 如图,已知△AOB,∠AOB=
如图,已知△AOB,∠AOB=