题目内容
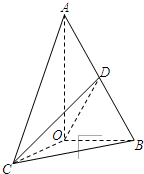 如图,已知△AOB,∠AOB=
如图,已知△AOB,∠AOB=| π |
| 2 |
| π |
| 6 |
(Ⅰ) 当平面COD⊥平面AOB时,求θ的值;
(Ⅱ) 当θ∈[
| π |
| 2 |
| 2π |
| 3 |
分析:解法一(向量法):(I)以O为原点,在平面OBC内垂直于OB的直线为x轴,OB,OA所在的直线分别为y轴,z轴建立空间直角坐标系O-xyz,我们分别求出平面COD和平面AOB的法向量,根据两个向量垂直则两个向量的数量积为0,可构造关于θ的方程,代入即可得到θ的值;
(II)设二面角C-OD-B的大小为α,根据θ∈(
,
],cosα=
,我们易确定出cosα的范围,即二面角C-OD-B的余弦值的取值范围.
解法二(几何法):(I)在平面AOB内过B作OD的垂线,垂足为E,根据平面COD⊥平面AOB,由面面垂直及线面垂直的性质,结合二面角的定义,即可得到二面角B-AO-C的平面角为∠COB,进而求出θ的值;
(Ⅱ)过C作OB的垂线,垂足为F,过F作OD的垂线,垂足为G,连接CG,则∠CGF的补角为二面角C-OD-B的平面角,根据θ∈[
,
],我们易求出cos∠CGF的取值范围.
(II)设二面角C-OD-B的大小为α,根据θ∈(
| π |
| 2 |
| 2π |
| 3 |
| ||||
|
|
解法二(几何法):(I)在平面AOB内过B作OD的垂线,垂足为E,根据平面COD⊥平面AOB,由面面垂直及线面垂直的性质,结合二面角的定义,即可得到二面角B-AO-C的平面角为∠COB,进而求出θ的值;
(Ⅱ)过C作OB的垂线,垂足为F,过F作OD的垂线,垂足为G,连接CG,则∠CGF的补角为二面角C-OD-B的平面角,根据θ∈[
| π |
| 2 |
| 2π |
| 3 |
解答: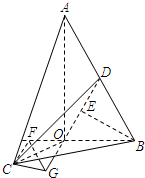 解法一:(Ⅰ) 如图,以O为原点,在平面OBC内垂直于OB的直线为x轴,OB,OA所在的直线分别为y轴,z轴建立空间直角坐标系O-xyz,则A (0,0,2
解法一:(Ⅰ) 如图,以O为原点,在平面OBC内垂直于OB的直线为x轴,OB,OA所在的直线分别为y轴,z轴建立空间直角坐标系O-xyz,则A (0,0,2
),B (0,2,0),
D (0,1,
),C (2sinθ,2cosθ,0).
设
=(x,y,z)为平面COD的一个法向量,
由
得
取z=sinθ,则
=(
cosθ,-
sinθ,sinθ).因为平面AOB的一个法向量为
=(1,0,0),由平面COD⊥平面AOB得
•
=0,
所以cosθ=0,即θ=
. …(7分)
(Ⅱ) 设二面角C-OD-B的大小为α,由(Ⅰ)得当θ=
时,cosα=0;
当θ∈(
,
]时,tanθ≤-
,cosα=
=
=-
,
故-
≤cosα<0.综上,二面角C-OD-B的余弦值的取值范围为[-
,0]. (14分)
解法二:(Ⅰ) 解:在平面AOB内过B作OD的垂线,垂足为E,因为平面AOB⊥平面COD,
平面AOB∩平面COD=OD,所以BE⊥平面COD,故BE⊥CO.
又因为OC⊥AO,所以OC⊥平面AOB,故OC⊥OB.
又因为OB⊥OA,OC⊥OA,所以二面角B-AO-C的平面角为∠COB,
即θ=
. …(7分)
(Ⅱ) 解:当θ=
时,二面角C-OD-B的余弦值为0;当θ∈(
,
]时,
过C作OB的垂线,垂足为F,过F作OD的垂线,垂足为G,连接CG,
则∠CGF的补角为二面角C-OD-B的平面角.在Rt△OCF中,CF=2 sinθ,OF=-2cosθ,
在Rt△CGF中,GF=OF sin
=-
cosθ,CG=
,
所以cos∠CGF=
=-
.因为θ∈(
,
],tanθ≤-
,
0<cos∠CGF=
≤
.余弦值的取值范围为[-
,0]. …(14分)
 解法一:(Ⅰ) 如图,以O为原点,在平面OBC内垂直于OB的直线为x轴,OB,OA所在的直线分别为y轴,z轴建立空间直角坐标系O-xyz,则A (0,0,2
解法一:(Ⅰ) 如图,以O为原点,在平面OBC内垂直于OB的直线为x轴,OB,OA所在的直线分别为y轴,z轴建立空间直角坐标系O-xyz,则A (0,0,2| 3 |
D (0,1,
| 3 |
设
| n1 |
由
|
|
取z=sinθ,则
| n1 |
| 3 |
| 3 |
| n2 |
| n1 |
| n2 |
所以cosθ=0,即θ=
| π |
| 2 |
(Ⅱ) 设二面角C-OD-B的大小为α,由(Ⅰ)得当θ=
| π |
| 2 |
当θ∈(
| π |
| 2 |
| 2π |
| 3 |
| 3 |
| ||||
|
|
| ||
|
| ||
|
故-
| ||
| 5 |
| ||
| 5 |
解法二:(Ⅰ) 解:在平面AOB内过B作OD的垂线,垂足为E,因为平面AOB⊥平面COD,
平面AOB∩平面COD=OD,所以BE⊥平面COD,故BE⊥CO.
又因为OC⊥AO,所以OC⊥平面AOB,故OC⊥OB.
又因为OB⊥OA,OC⊥OA,所以二面角B-AO-C的平面角为∠COB,
即θ=
| π |
| 2 |
(Ⅱ) 解:当θ=
| π |
| 2 |
| π |
| 2 |
| 2π |
| 3 |
过C作OB的垂线,垂足为F,过F作OD的垂线,垂足为G,连接CG,
则∠CGF的补角为二面角C-OD-B的平面角.在Rt△OCF中,CF=2 sinθ,OF=-2cosθ,
在Rt△CGF中,GF=OF sin
| π |
| 3 |
| 3 |
| 4sin2θ+3cos2θ |
所以cos∠CGF=
| FG |
| CG |
| ||
|
| π |
| 2 |
| 2π |
| 3 |
| 3 |
0<cos∠CGF=
| ||
|
| ||
| 5 |
| ||
| 5 |
点评:本题考查的知识点是与二面角有关的立体几何问题,平面与平面垂直的性质,其中向量的关键是建立适当的空间坐标系,将空间面面垂直关系转化为向量垂直问题,将二面角问题转化为向量夹角问题,几何法中(I)的关键是确定出二面角B-AO-C的平面角为∠COB,∠CGF的补角为二面角C-OD-B的平面角.

练习册系列答案
相关题目

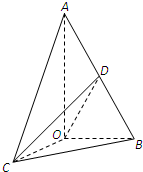 (2011•江西模拟)如图,已知△AOB,∠AOB=
(2011•江西模拟)如图,已知△AOB,∠AOB= 如图,已知△AOB,∠AOB=
如图,已知△AOB,∠AOB=