题目内容
不等式cos2x>sin2x的解集为
- A.
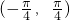
- B.

- C.

- D.
 以上k∈Z
以上k∈Z
B
分析:先将sin2x<cos2x化为cos2x-sin2x>0,就是cos2x>0,然后求解不等式即可得到x的取值范围.
解答:∵sin2x<cos2x,
∴cos2x-sin2x>0,
由二倍角公式可得,cos2x>0
∴ ,k∈Z
,k∈Z
解得:
所以x的取值范围是
故选B
点评:本题考查余弦函数的单调性,二倍角的余弦,考查计算能力,是中档题.
分析:先将sin2x<cos2x化为cos2x-sin2x>0,就是cos2x>0,然后求解不等式即可得到x的取值范围.
解答:∵sin2x<cos2x,
∴cos2x-sin2x>0,
由二倍角公式可得,cos2x>0
∴
 ,k∈Z
,k∈Z解得:

所以x的取值范围是

故选B
点评:本题考查余弦函数的单调性,二倍角的余弦,考查计算能力,是中档题.

练习册系列答案
相关题目
 )sin(
)sin( )+m>0恒成立,求实数m的取值范围.
)+m>0恒成立,求实数m的取值范围.