题目内容
12.已知实数x,y满足|x-y+2|≤1,|3x-2y|≤3,则|5x+4|的最大值为49.分析 通过解含有绝对值的表达式可知-3≤x-y≤-1、-3≤3x-2y≤3,画出图象、计算可知C(9,12),进而计算即得结论.
解答 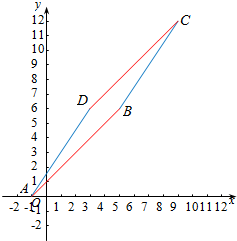 解:∵|x-y+2|≤1,
解:∵|x-y+2|≤1,
∴-3≤x-y≤-1,
∵|3x-2y|≤3,
∴-3≤3x-2y≤3,
∴联立$\left\{\begin{array}{l}{x-y=-3}\\{3x-2y=-3}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=9}\\{y=12}\end{array}\right.$,即C(9,12),
∴|5x+4|的最大值为|5×9+4|=49,
故答案为:49.
点评 本题是一道简单随机规划题,涉及到含有绝对值的表达式,考查数形结合能力,注意解题方法的积累,属于中档题.

练习册系列答案
相关题目
2.直线l1,l2在x轴上的截距都是m,在y轴上的截距都是n,则11与l2( )
| A. | 平行 | B. | 重合 | C. | 平行或重合 | D. | 相交或重合 |
5.【文】设双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{8}$=1(a>0)的左、右焦点分别为F1、F2,其一条渐近线与圆(x-a)2+y2=4相切于点M,则△F1MF2的面积为( )
| A. | 4$\sqrt{2}$ | B. | 2$\sqrt{2}$ | C. | 8 | D. | 4 |
10.如图在边长为1的正方形网格中用粗线画出了某个多面体的三视图,则该多面体的表面积为( )
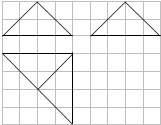

| A. | 8+12$\sqrt{2}$ | B. | 16+24$\sqrt{2}$ | C. | $\frac{1}{3}(8+12\sqrt{2})$ | D. | 4+6$\sqrt{2}$ |
