题目内容
设{xn}是各项都为正数的等比数列,{yn}是等差数列,且x1=y1=1,x3+y5=13,x5+y3=21.
(1)求{xn},{yn}的通项公式.
(2)若i,j均为正整数,且1≤i≤j≤n,求所有可能乘积xi•yj的和S.
(1)求{xn},{yn}的通项公式.
(2)若i,j均为正整数,且1≤i≤j≤n,求所有可能乘积xi•yj的和S.
分析:(1)直接根据x3+y5=13,x5+y3=21列出关于公差和公比的等式,解方程求出公差和公比,即可求出通项公式.
(2)先根据条件得到S=x1•y1+(x1+x2)•y2+…+(x1+x2+…+xn)•yn;再求出(x1+x2+…+xn)•yn的通项;最后利用错位相减以及裂项求和法求出结果.
(2)先根据条件得到S=x1•y1+(x1+x2)•y2+…+(x1+x2+…+xn)•yn;再求出(x1+x2+…+xn)•yn的通项;最后利用错位相减以及裂项求和法求出结果.
解答:解:(1)设{xn}的公比为q(q>0),{yn}的公差为d,
则
得d=2,q=2,
所以:xn=2n-1,yn=2n-1.
(2)由题意S=x1•y1+(x1+x2)•y2+…+(x1+x2+…+xn)•yn…
研究通项:
…
∴S=[1•2+3•22+…+(2n-1)•2n]-
令Tn=1•2+3•22+…+(2n-1)•2n;
2Tn=1•22+3•23+…+(2n-1)•2n+1
由错位相减法得:Tn=(2n-3)•2n+1+6,
∴S=(2n-3)•2n+1+6-n2.
则
|
所以:xn=2n-1,yn=2n-1.
(2)由题意S=x1•y1+(x1+x2)•y2+…+(x1+x2+…+xn)•yn…
研究通项:
|
∴S=[1•2+3•22+…+(2n-1)•2n]-
| n(1+2n-1) |
| 2 |
令Tn=1•2+3•22+…+(2n-1)•2n;
2Tn=1•22+3•23+…+(2n-1)•2n+1
由错位相减法得:Tn=(2n-3)•2n+1+6,
∴S=(2n-3)•2n+1+6-n2.
点评:本题主要考察等差数列和等比数列的综合知识.其中涉及到数列求和的错位相减法以及分组求和法,这是数列求和的常用方法.

练习册系列答案
相关题目
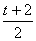 处取得最小值-
处取得最小值-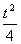 (t﹥0),f(1)=0, (1)求y=f(x)的表达式;(2)若任意实数x都满足等式f(x)g(x)+anx+bn=xn+1 (g(x)为多项式,n∈N+)试用t表示an和bn;(3)设圆Cn的方程为(x-an)2+(y-bn)2=r
(t﹥0),f(1)=0, (1)求y=f(x)的表达式;(2)若任意实数x都满足等式f(x)g(x)+anx+bn=xn+1 (g(x)为多项式,n∈N+)试用t表示an和bn;(3)设圆Cn的方程为(x-an)2+(y-bn)2=r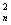 ,圆Cn与Cn+1
外切(n=1,2,3…),{rn}是各项都为正数的等比数列,记Sn为前n个圆的面积之和,求rn,sn。
,圆Cn与Cn+1
外切(n=1,2,3…),{rn}是各项都为正数的等比数列,记Sn为前n个圆的面积之和,求rn,sn。