题目内容
(本小题满分12分)已知数列 满足
满足 ,
, ;数列
;数列 满足
满足 ,
, ,且
,且 为等差数列.
为等差数列.
(Ⅰ)求数列 和
和 的通项公式;
的通项公式;
(Ⅱ)求数列 的前
的前 项和
项和 .
.
(Ⅰ) ,
, ; (Ⅱ)
; (Ⅱ)
【解析】
试题分析:(Ⅰ)首先利用等比数列的通项公式得: ,再利用数列
,再利用数列 和
和 的关系求出
的关系求出 的通项公式;(Ⅱ)根据数列
的通项公式;(Ⅱ)根据数列 的通项公式结构特点,可采用拆项分组的方法,把变成一个等差数列前n项和一个等比数列的前n项和问题.
的通项公式结构特点,可采用拆项分组的方法,把变成一个等差数列前n项和一个等比数列的前n项和问题.
试题解析:.【解析】
(Ⅰ)由题意知数列 是首项
是首项 ,公比
,公比 的等比数列,
的等比数列,
所以 ;
;
因为 ,
, ,
,
所以数列 的公差为
的公差为 .
.
所以 .
.
所以 . (6分)
. (6分)
(Ⅱ)


 . (12分)
. (12分)
考点:等差数列与等比数列.

练习册系列答案
 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案
相关题目
 ,(
,(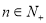 ),则在数列{
),则在数列{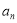 }的前50项中最小项和最大项分别是( )
}的前50项中最小项和最大项分别是( )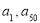 B.
B.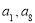 C.
C.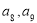 D.
D.
 ,则
,则 的大小关系是( )
的大小关系是( ) B.
B.  C.
C.  D.
D. 
 的左、右顶点分别为A、B,点P是第一象限内双曲线上的点。若直线PA、PB的倾斜角分别为α、β,且
的左、右顶点分别为A、B,点P是第一象限内双曲线上的点。若直线PA、PB的倾斜角分别为α、β,且 ,那么α的值是( )
,那么α的值是( ) B.
B. C.
C.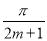 D.
D.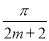
 (其中
(其中 为虚数单位)的虚部等于( )
为虚数单位)的虚部等于( ) B.
B.  C.
C. D.
D.
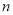 的值为100,则输出S的值为_______.
的值为100,则输出S的值为_______.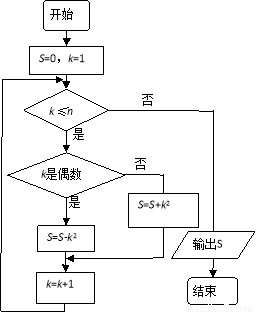
 满足
满足 ,则
,则 的所有可能值为
的所有可能值为 B.
B. C.1 D.1或
C.1 D.1或
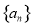 的通项公式是_______.
的通项公式是_______.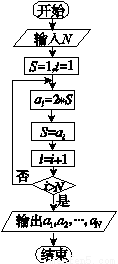
 的左焦点为
的左焦点为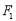 ,点
,点 是椭圆上异于顶点的任意一点,
是椭圆上异于顶点的任意一点,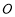 为坐标原点.若点
为坐标原点.若点 是线段
是线段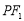 的中点,则
的中点,则 的周长为 .
的周长为 .