题目内容
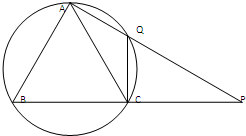（2013•渭南二模）（选做题）在圆内接△ABC中，AB=AC=5| 3 |
15
15
．分析：连接BQ，可由∠AQB=∠ABP和∠BAQ=∠PAB，证出△AQB∽△ABP，所以AB2=AP•AQ，再代入题中所给数据，可得AP=15．
解答：
解：连接BQ
∵∠ACB与∠AQB同对弧AB，∴∠ACB=∠AQB
又∵AB=AC，∴∠ACB=∠ABC
∴∠AQB=∠ABP
∵∠BAQ=∠PAB，
∴△AQB∽△ABP，可得
=
，即AB2=AP•AQ
∵AB=5
，AQ：QP=1：2，
∴（5
）2=AP•
AP，即AP2=225，可得AP=15
故答案为：15
解：连接BQ∵∠ACB与∠AQB同对弧AB，∴∠ACB=∠AQB
又∵AB=AC，∴∠ACB=∠ABC
∴∠AQB=∠ABP
∵∠BAQ=∠PAB，
∴△AQB∽△ABP，可得
| AQ |
| AB |
| AB |
| AP |
∵AB=5
| 3 |
∴（5
| 3 |
| 1 |
| 3 |
故答案为：15
点评：本题给出圆内接等腰三角形和一条被圆分为1：2两部分的割线，要我们求割线的长，着重考查了三角形相似和与圆有关的比例线段等知识，属于中档题．
练习册系列答案
智慧小复习系列答案
相关题目
（2013•渭南二模）某几何体的主视图与俯视图如图所示，左视图与主视图相同，且图中的四边形都是边长为2的正方形，两条虚线互相垂直，则该几何体的体积是（ ）